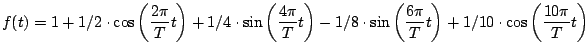Nächste Seite: Kenntnisse von Funktionen mehrerer
Aufwärts: Selbsttest zum Kapitel 5
Vorherige Seite: Selbsttest zum Kapitel 5
Inhalt
- T511
- Verständnisfragen
- -
- Wieso setzt man die Gleichstromkomponente als
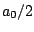 in die Formel?
in die Formel?
- -
- Wodurch können sich z.B. zwei Zeitfunktionen
unterscheiden, welche dasselbe Powerspektrum haben?
- -
- Wieviele Koeffizienten kann eine Fourier-Darstellung
maximal enthalten, wenn dies bis zur 10. Harmonischen geht?
- -
- Wie kann man einen einzelnen komplexen Koeffizienten
z.B.
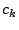 in einer Fourierreihe ersetzen, wenn man sonst alle
komplexen Koeffizienten kennt?
in einer Fourierreihe ersetzen, wenn man sonst alle
komplexen Koeffizienten kennt?
- T512
- Führen Sie die einfache Faltung der Folgen
a=[1 2 3 4] und b = [1 0 1 1 0 1] mit
Bleistift und Papier durch, sowohl als
direkte einfache Faltung, als auch als zirkuläre Faltung bei welcher
die notwendige Anzahl Nullen angehängt wurde. Vergleichen Sie
die Resultate.
- T513
- Geben Sie die Amplituden-Phasen-Darstellung, das Powerspektrum
und die komplexen Koeffizienten an
für die Fourier-Reihe:
- T514
- Überlegen Sie sich, vorerst ohne nachzuschauen,
wie die komplexe Matrix zu einer DFT von 4 Punkten, k=0 bis 3
aussieht.
- T515
- Schreiben Sie ein MATLAB-Skript, das
durch Punkt-Multiplikation und Summation mit Funktionen der Art
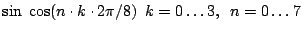 zu einer tabellarisch
gegebenen Funktion von 8 Werten die DFT bestimmt.
zu einer tabellarisch
gegebenen Funktion von 8 Werten die DFT bestimmt.




Nächste Seite: Kenntnisse von Funktionen mehrerer
Aufwärts: Selbsttest zum Kapitel 5
Vorherige Seite: Selbsttest zum Kapitel 5
Inhalt
Stefan Adam
2006-03-07
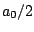 in die Formel?
in die Formel?
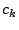 in einer Fourierreihe ersetzen, wenn man sonst alle
komplexen Koeffizienten kennt?
in einer Fourierreihe ersetzen, wenn man sonst alle
komplexen Koeffizienten kennt?