Testserie 7.1

T711

Verständnisfragen

-

Wodurch unterscheidet sich ein Quadraturproblem von einer ,,eigentlichen`` Differentialgleichung?

-

Wieviele Differentialgleichungen 1. Ordnung umfasst ein System zur Lösung von drei Differentialgleichungen, die jede von 2. Ordnung sind? (z.B. Bewegungsgleichungen eines Massenpunktes im Raum.)

-

Die ode-Prozeduren in MATLAB benützen alle eine interne Schrittweitensteuerung beim Suchen der Lösung. Worauf muss man deshalb bei der grafischen Darstellung der Resultate achten?

-

Warum muss man beim Erstellen der Funktion zur Bestimmung der Ableitungen einen Eingabeparameter mit der aktuellen unabhängigen Variablen (i.A. der Zeit) in die Parameterliste aufnehmen, auch wenn man diesen Wert bei autonomen Systemen gar nicht benötigt?

T712

Stellen Sie die M-Files zusammen, welche die Differentialgleichung der Entleerung eines vertikal stehenden zylindrischen Tanks von 2.6 m Durchmesser und 3.5 m Höhe durch eine Öffnung von 80 mm Durchmesser beschreiben! Die Ausflussgeschwindigkeit kann mit 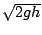$\sqrt{2gh}$ angenähert werden. (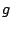$g$ Erdbeschleunigung, 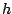$h$ Flüssigkeitsstand über Ausfluss)

T713

Erstellen Sie die M-Files zur Beschreibung der Bahnen von elektrisch geladenen Teilchen in der Ebene, zu welcher ein Magnetfeld mit der Stärke proportional zur x-Koordinate senkrecht steht.

T714

Zum folgenden System von Differentialgleichungen

mit den Anfangsbedingungen

$x(0) = 0$

$\dot x (0) = 1.0$

und

$y(0) = 20$

$\dot y (0) = 0$

soll das zugehörige System 1. Ordnung bestimmt werden. Anschließend sind zwei Lösungsschritte nach dem Euler-Verfahren mit je einer Schrittweite von 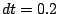$dt=0.2$ durchzurechnen.

T715

Erstellen Sie die M-Files für die Differentialgleichung des freien Falls: a) unter Vernachlässigung des Luftwiderstandes, und b) unter Einbezug einer Bremskraft 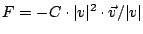$F = - C\cdot \vert v\vert^2 \cdot \vec{v}/\vert v\vert$, die proportional zur Geschwindigkeit ist.