



Nächste Seite: Testserie 4.2
Aufwärts: Selbsttests zum Kapitel 4
Vorherige Seite: Selbsttests zum Kapitel 4
Inhalt
- T411
- Verständnisfragen
- -
- Wie kann man das Skalarprodukt zur Bestimmung der Länge eines
Vektors einsetzen?
- -
- Welche Elemente einer 3x3 Matrix für die
homogene Koordinatentransformation der Ebene sind von vornherein festgelegt?
- -
- Wie sieht die Matrix für die Punktspiegelung
am Koordinatenursprung der Ebene in homogenen Koordinaten aus?
- -
- Wie erzeugt man aus einem Vektor eine Projektionsmatrix, welche
einen beliebigen räumlichen Vektor auf den vorgegebenen
Vektor projiziert?
- T412
- Bestimmen Sie
die Durchstoßpunkte der Geraden
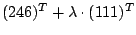 durch die drei Koordinatenebenen xy, xz und yz.
durch die drei Koordinatenebenen xy, xz und yz.
- T413
- Bestimmen Sie die
Gleichung in der Hesse'schen Normalform für die
Ebene E durch die drei Punkte A
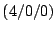 , B
, B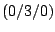 , C
, C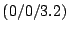 . Bestimmen
Sie ebenfalls die Gleichung der dazu parallelen Ebene F, welche
den doppelten Abstand zum Koordinatenursprung aufweist wie E.
. Bestimmen
Sie ebenfalls die Gleichung der dazu parallelen Ebene F, welche
den doppelten Abstand zum Koordinatenursprung aufweist wie E.
- T414
- Berechnen Sie die wahre Neigung
der Ebenen ABC und ABD, sowie den Winkel zwischen
diesen beiden Ebenen. A(0/0/0), B(2/2/8), C(10/0/0), D(0/4/0).
- T415
- Erarbeiten Sie die Matrizen der Gesamttransformationen
in homogenen Koordinaten der Ebene für die Rotation
des Quadrates ABCD (A(0/0), B(8/0), C(8/8)) um seinen Mittelpunkt, für die
Drehwinkel 90
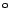 , 180
, 180
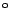 und 270
und 270
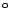 .
Testen Sie die Behauptung, dass das Quadrat durch jede der Abbildungen in
sich selbst übergeht.
.
Testen Sie die Behauptung, dass das Quadrat durch jede der Abbildungen in
sich selbst übergeht.




Nächste Seite: Testserie 4.2
Aufwärts: Selbsttests zum Kapitel 4
Vorherige Seite: Selbsttests zum Kapitel 4
Inhalt
Stefan Adam
2006-03-07