



Nächste Seite: Faltungs- und Fourier-Theorie aktivieren
Aufwärts: Selbsttests zum Kapitel 4
Vorherige Seite: Testserie 4.1
Inhalt
- T421
- Verständnisfragen
- -
- Welchem Wert entspricht der Betrag der Kreuzproduktes?
- -
- Die Matrizen für kongruente Abbildungen der Ebene und des Raumes
in gewöhnlichen Koordinaten (und damit die Teilmatrizen in der
linken oberen Ecke bei homogenen Transformationen) gehören alle zu
einem speziellen Matrizen-Typ. Zu welchem?
- -
- Wie sieht die Matrix für eine Drehung um den
Koordinatenursprung der Ebene um 90
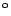 in homogenen Koordinaten aus?
in homogenen Koordinaten aus?
- -
- Für zwei parallele Ebenen seien die Terme
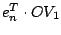 bzw.
bzw.
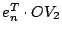 von verschiedenem Vorzeichen. Was bedeutet das für die
Lage dieser zwei Ebenen in Bezug auf den Koordinatenursprung?
von verschiedenem Vorzeichen. Was bedeutet das für die
Lage dieser zwei Ebenen in Bezug auf den Koordinatenursprung?
- T422
- Bestimmen Sie kürzeste Verbindung zwischen
den windschiefen Geraden g:
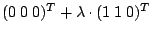 h:
h:
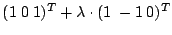 !
!
- T423
- Bestimmen Sie Distanz des Koordinatenursprungs von der
Ebene E durch die drei Punkte A
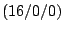 , B
, B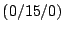 , C
, C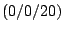 ,
sowie den Fusspunkt des Lotes vom Koordinatenursprung
auf diese Ebene!
,
sowie den Fusspunkt des Lotes vom Koordinatenursprung
auf diese Ebene!
- T424
- Berechnen Sie die wahre Neigung der Seitenflächen
und der Kanten für einen auf seiner Grundfläche stehenden
regulären Tetraeder!
- T425
- Erstellen Sie ein M-File zum Zeichnen eines
achtstrahligen Windrädchens mit Mittelpunkt (10/10) und der
Flügelform entsprechend dem Dreieck
(A(0/0), B(8/0), C(2/2))!




Nächste Seite: Faltungs- und Fourier-Theorie aktivieren
Aufwärts: Selbsttests zum Kapitel 4
Vorherige Seite: Testserie 4.1
Inhalt
Stefan Adam
2006-03-07
 in homogenen Koordinaten aus?
in homogenen Koordinaten aus?
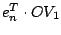 bzw.
bzw.
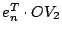 von verschiedenem Vorzeichen. Was bedeutet das für die
Lage dieser zwei Ebenen in Bezug auf den Koordinatenursprung?
von verschiedenem Vorzeichen. Was bedeutet das für die
Lage dieser zwei Ebenen in Bezug auf den Koordinatenursprung?