



Nächste Seite: Logische Operatoren angewandt auf
Aufwärts: Übungen zum Kapitel 1
Vorherige Seite: Fachausdrücke zur Matrizentheorie
Inhalt
Unterabschnitte
Sehen Sie Sich die Resultate der MATLAB-Funktionen zeros(k), ones(k), eye(k)
an
für verschiedene quadratische Dimensionszahlen 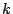 , z.B.
, z.B.
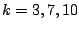 .
.
Wenden Sie zeros() und ones() zum Erzeugen einer nxm Rechtecksmatrix an.
Erzeugen Sie das Komplement zur Einheitsmatrix mit Nullen auf der Diagonalen
und Einsen an den anderen Plätzen.
Sehen Sie in der Hilfefunktion nach, wie diag() anzuwenden ist.
Erzeugen Sie anschließend eine Diagonalmatrix der Dimension nxn z.B. 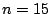 mit den fortlaufenden ungeraden Zahlen
mit den fortlaufenden ungeraden Zahlen 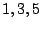 etc. in der Diagonalen.
etc. in der Diagonalen.
Verwenden Sie das Prinzip, dass man Matrizen aus kleineren
Matrizen zusammenfügen kann, um
quadratische Matrizen der Dimension
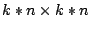 (
(
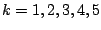 ), (
), (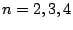 )
zu erzeugen, welche auf der Diagonalen
und auf
)
zu erzeugen, welche auf der Diagonalen
und auf 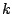 parallelen Linien im Abstand
parallelen Linien im Abstand 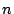 dazu je Einsen haben und sonst Nullen. (Lauter Matrizen die mit
eye(n) erzeugt wurden, werden zusammengefügt.)
dazu je Einsen haben und sonst Nullen. (Lauter Matrizen die mit
eye(n) erzeugt wurden, werden zusammengefügt.)
Benutzen Sie die Funktion spy(M) zur grafischen Darstellung der von
Null verschiedenen Werte einer Matrix. Diese Funktion ist besonders
beim Arbeiten mit dünn besetzten Matrizen (englisch: sparse matrices) wertvoll.
Lernen Sie die MATLAB-Demo über magische Quadrate (Demo - Matrizen -
Matrix-Manipulationen) kennen! Nehmen Sie daraus
ein magischer Quadrat 3x3 oder 4x4 und probieren Sie das folgende Rezept aus:
Ein magisches Quadrat der Dimension nxn kann man wie folgt quadrieren:
In die nxn Teilmatrix am Platz (j,k) setzt man die Originalmatrix ein,
plus den ,,Sockelwert``
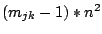 : dies ergibt ein magisches
Quadrat der Dimensionen
: dies ergibt ein magisches
Quadrat der Dimensionen
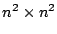 .
.




Nächste Seite: Logische Operatoren angewandt auf
Aufwärts: Übungen zum Kapitel 1
Vorherige Seite: Fachausdrücke zur Matrizentheorie
Inhalt
Stefan Adam
2006-03-07