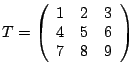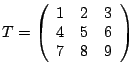Nächste Seite: Hilfsfunktionen zum Erzeugen von
Aufwärts: Übungen zum Kapitel 1
Vorherige Seite: Matrixdefinition
Inhalt
Unterabschnitte
- -
- Eine symmetrische Matrix ist quadratisch.
- -
- Eine antisymmetrische Matrix, addiert zu ihrer Transponierten ergibt die
Nullmatrix.
- -
- Eine Matrix mit lauter Nullen ist das Neutralelement
der Matrixmultiplikation.
- -
- Jede Diagonalmatrix ist regulär.
- -
- Das Produkt quadratische Matrix mal Spaltenvektor ergibt
wieder einen Spaltenvektor, falls die Multiplikation möglich ist.
- -
- Das Produkt einer Rechtecksmatrix mit ihrer
Transponierten ist immer möglich und ergibt eine quadratische Matrix.
- -
- Jede symmetrische Matrix ist mit ihrer Transponierten identisch.
Berechnen Sie aus der Matrix 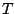 den Ausdruck
den Ausdruck 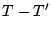 !
Suchen Sie eine Methode, um den antisymmetrischen
!
Suchen Sie eine Methode, um den antisymmetrischen 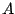 und
den symmetrischen Anteil
und
den symmetrischen Anteil 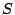 der Matrix
der Matrix 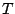 zu bestimmen, so dass gilt
zu bestimmen, so dass gilt 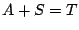 !
!
Finden Sie je eine 3x3 Matrix der folgenden Typen:
symmetrische Matrix, antisymmetrische Matrix, Nullmatrix, Diagonalmatrix,
Einheitsmatrix, obere
Dreiecksmatrix, untere Dreiecksmatrix.
Bestimmen Sie von jedem Typ die Anzahl Freiheitsgrade.
Suchen Sie möglichst viele Teilmengenrelationen der Art: ,,Die Einheitsmatrix
bildet eine Teilmenge der Diagonalmatrizen.``




Nächste Seite: Hilfsfunktionen zum Erzeugen von
Aufwärts: Übungen zum Kapitel 1
Vorherige Seite: Matrixdefinition
Inhalt
Stefan Adam
2006-03-07