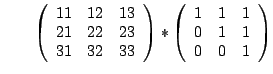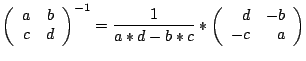Nächste Seite: Formulieren von Gleichungssystemen in
Aufwärts: Übungen zum Kapitel 1
Vorherige Seite: Logische Operatoren angewandt auf
Inhalt
Unterabschnitte
Berechnen Sie von Hand die Matrizenprodukte
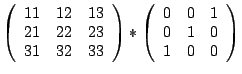 und und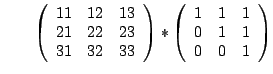 |
|
und kontrollieren Sie Ihr Resultat mit Hilfe von MATLAB!
Multiplizieren Sie mit Bleistift und Papier je eine 2x2 und eine 3x3 Matrix
deren Werte die Indizes als zweistellige Zahlen enthalten, jeweils von
links und von rechts mit einer
allgemeinen Matrix mit den Werten 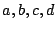 bzw.
bzw. 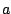 bis
bis 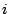 .
.
Multiplizieren Sie mit Hilfe von Bleistift und Papier
eine 2x2 Matrix D mit den Zahlen (1..4) mit
sich selbst (d.h. berechnen Sie D*D von Hand).
Multiplizieren Sie ebenso die 3x3 Matrix T mit
den Zahlen (1..9) mit sich selbst.
Prüfen Sie die Resultate mit MATLAB.
Multiplizieren Sie mit Bleistift und Papier die zwei allgemeinen
2x2 Matrizen [a b ; c d] und [u v ; w x ].
Bestimmen Sie
aus der Forderung, dass das Resultat die Einheitsmatrix [1 0; 0 1]
ergeben muss vier Gleichungen, welche die
Parameter 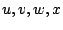 als Funktion von
als Funktion von 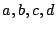 erfüllen müssen.
erfüllen müssen.
Durch Auflösen dieser vier Gleichungen nach 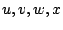 erhält man eine
geschlossenen formelmäßige Lösung für
die Inverse einer 2x2 Matrix.
erhält man eine
geschlossenen formelmäßige Lösung für
die Inverse einer 2x2 Matrix.
Mit den 4 Matrizen / Vektoren A 2x3, B 3x3, v 3x1, w 2x1 sollen
die folgenden Operationen auf ihre Legalität überprüft werden:
-
- A+B A+A B+B v+w w-v
A*B B*A A'*B B*A'
A*v v*A v*A' w*A' v*v' v'*v B*v B*w A'*v
A*A A'*A A*A' B*B
Bilden Sie alle möglichen Rechtecksmatrizen, welche die Zahlen 1 bis 6
der Reihe nach enthalten, also E 1x6, Z 2x3, D 3x2 und S 6x1.
Bilden Sie zusätzlich deren Transponierte Et=E', Zt, etc. und suchen Sie
alle legalen Multiplikationen, welche zwischen zwei von diesen 8 Matrizen
möglich sind! Bestimmen Sie jeweils die Resultat-Dimensionen.
Erzeugen Sie die vier Matrizen. bzw. Vektoren A(4x3), N(3x3), v(3x1),
w(1x4), so dass die darin enthaltenen Zahlen den
Index als zweistellige Zahl darstellen (z.B.
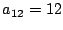 ,
,
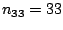 ).
Prüfen Sie mit MATLAB, welche der folgenden Multiplikationen legal sind
und überlegen Sie sich jeweils vorgängig, ob Sie den Fall
als legal eingestuft hätten: (M' steht für
).
Prüfen Sie mit MATLAB, welche der folgenden Multiplikationen legal sind
und überlegen Sie sich jeweils vorgängig, ob Sie den Fall
als legal eingestuft hätten: (M' steht für 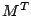 , d.h.
M-transponiert)
, d.h.
M-transponiert)
-
- w*A, w'*A, w*A', w'*A', A*w, A*w', A'*w, A'*w'
w*w, w*w', w'*w, v*v, v'*v, v*v'
N*v, v*N, v'*N, N*v'
A*N, A*N', A'*N, A'*N'
Zeigen Sie durch Nachrechnen von Hand, dass gilt:




Nächste Seite: Formulieren von Gleichungssystemen in
Aufwärts: Übungen zum Kapitel 1
Vorherige Seite: Logische Operatoren angewandt auf
Inhalt
Stefan Adam
2006-03-07
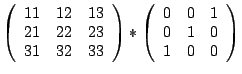 und
und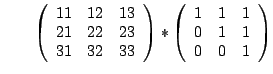
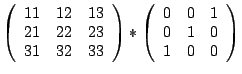 und
und