Lösungshinweise zum Kapitel 1

Im Text eingebettete Übungen

 

11-1 $\mathrm{e} = \mathrm{e}^1$ = exp(1).

12-1 Allgemeine nxm Matrix: n*m Freiheitsgrade. Diagonalmatrix, nxn: n FG.
Obere Dreiecksmatrix nxn: $n*(n+1)/2$ FG.
Das ist $n^2/2$ plus halbe Diagonale = $n^2/2 + n/2 = n(n+1)/2$.
Gleichzeitig obere und untere Dreiecksmatrix: Diagonalmatrix.
Gewöhnlicher (Spalten-) Vektor ist eine hohe Matrix.
Nebendiagonalen in nxn, je n-1, also total 2*n-2.
``Indicating the size of a matrix, the number of rows is followed by the number of columns.''

12-2 4x5 Matrix: rechts oben (1,5); rechts unten (4,5); links unten (4,1); Mitte der untersten Zeile (4,3).

12-3 Eine 4x4 Matrix hat in der Diagonalen die Indizes (1,1), (2,2), (3,3) und (4,4).

12-4 $$z^T = \left( \begin{array}{r} 1\\ 2\\ 3\\ 4 \end{array}\... ...begin{array}{rr} 1 & 10\\ 2 & 20\\ 3 & 30 \end{array}\right)$$

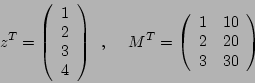
12-5 $$A = \left( \begin{array}{rrr} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 &... ...y}{rrr} 2 & 4 & 6\\ 8 &10 &12\\ 14&16 &18 \end{array}\right)$$
$$A+A^T = \left( \begin{array}{rrr} 2 & 6 & 10\\ 6 & 10 & 14... ...rrr} 0 & -2 & -4\\ 2 & 0 & -2\\ 4 & 2 & 0 \end{array}\right)$$

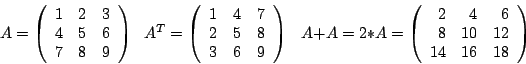
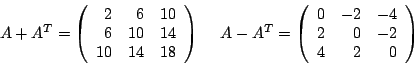
12-6 $$A*A^T = \left( \begin{array}{rrr} 14 & 32 & 50\\ 32 & 77 &... ... 78 & 90\\ 78 & 93 & 108\\ 90 & 108 & 126 \end{array}\right)$$
$$A*A = \left( \begin{array}{rrr} 30 & 36 & 42\\ 66 & 81 & 96\\ 102 & 126 & 150 \end{array}\right)$$

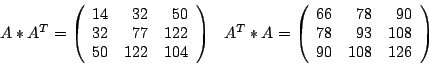
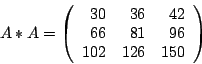
13-1 M=[3 2 1; 0 1 -1; 0 1 1]; b = [33 9 11]';
x=M\b ; x=[4 10 1]'

13-2 M= [1 -1 0 0; 0 1 -1 0; 0 0 1 -1; 1 0 0 1];
b = [4 2 1 0]'; x = [3.5 -0.5 -2.5 -3.5]'

13-3 M = [1 -1 1 -3; 0 1 -1 2; 0 0 1 -1; 0 0 0 1];
b = [0 4 3 2]'; x = [6 5 5 2]'

13-4 v = [4634 4478 3820 1620 678]' ; A = v*ones(1,5);
D = A'-A

Einfache Berechnungen

 

10-1 r[m] = 40000*1000/pi/2 = 6.366E06, V[m3] = 1.0808E21 rho [t/m3] = 5.97E21/1.0808E21 = 5.52

10-2 w = 30/360/60*2*pi = 0.009018, DL = w*384400 = 1733 km, DH = w*150E06 = 1.35E06 km

10-3 r=sqrt(2)*160/2 = 162.6 m, V=r*r*pi*320 = 1.26E07 m3, MLuft = V*0.0012 = 15400 t > MEisen

10-4 P = m*g*h/t = 75*9.81*300/3600 = 61.3 W

10-5 md = 24*60 = 1440,   sd = md*60 = 86400,   mw = md*7 = 10080,
sw = mw*7 = 70560,   my = md*365 = 525600,   sy = my*60 = 31536000,
hw = 24*7 = 168,   hy = 365*24 = 8760

10-6 20000/15*100 = 133333 km, mehr als 3 mal um die Erde.

10-7 300 $cm^3$ / (0.6 * 0.6) $cm^2$ = 833 cm = 8 Meter Pommes frites.
300/(0.1*0.1*pi) = 9549 cm = 95 m Spaghetti, also etwa 100 Meter.

Produktschreibweise mit '*'

 

10-8 Als Beispiel: a^4 - 4*a^3*b + 6*a^2*b^2 - 4*a*b^3 + b^4

Implizite Schleifen und Summen

 

10-9 Beispiel: Summe 1..99 = sum(1:99) = 99*100/2 = 4950

10-10 Beispiel: Summe 20:2:40 = 330 = 11*60/2

10-11 SMQL(3) = 15, SMQL(4) = 34, SMQL(6) = 111, SMQL(9) = 369

Matrixdefinition

 

10-12 Z01 = [ 1 2 ; 3 4 ], Z02 = [ 1 2 ; 4 3] , Z03 = [ 1 3; 2 4 ], Z04 =[ 1 3 ; 4 2 ], etc.
Z24 = [ 4 3; 2 1] , z.B. Z24 = flipud(filplr(Z01))

10-13 z.B. V = reshape(Z',3,4)'

10-14 Q = [ 1 0; 0 1], H = [Q Q; Q Q], S = [ H H; H H]

10-15 $$L = \left( \begin{array}{rrrr} 1 & 0 & 0 & 0\\ 1 & 1 & 0 &... ...1 & 1 & 1\\ 0 & 0 & 1 & 1\\ 0 & 0 & 0 & 1 \end{array}\right)$$

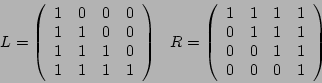
10-16 I6=eye(6), kurz = zeros(1,6), lang = zeros(1,7)
R7 = [ kurz' I6; lang], L7 = [lang; I6 kurz']

10-17 P=[] ;
for k=1:10
P = [P ; k:k:10*k];
end

10-18 v=[ 4 7 13 20 36 49 64 72 ]; e = ones(1,length(v));
H=v'*e; T = gcd(H,H'); V = lcm(H,H'); beide symmetrisch!
T .* V - v'*v (= Nullmatrix)

Fachausdrücke zur Matrizentheorie

 

10-19
- Ja, eine symmetrische Matrix ist quadratisch.
- Ja, denn durch Transponieren wechselt das Vorzeichen.
- Nein, sondern das Neutralelement der Addition, NE der Multiplikation ist I.
- Nein, eine Diagonalmatrix kann auch in der Diagonalen Nullen haben, dann ist sie singulär.
- Ja, (nxn)*(nx1) = (nx1), der Resultatvektor hat dieselbe Länge.
- Ja, (nxm)*(mxn) ist immer möglich und ergibt (nxn). Der ungewöhnlichste Fall (nx1)*(1xn) ergibt aus zwei Vektoren eine Matrix und heißt ,,dyadisches Produkt``.
- Ja, die Definition einer symmetrischen Matrix lautet gerade M' = M.

10-20 S = (T + T')/2 ; A = (T - T')/2

10-21 S: $n*(n+1)/2$ Fg.;  A: $n*(n-1)/2$ Fg.; 
Nl: 0 Fg.; D: n Fg.; I: 0 Fg.; R: $n*(n+1)/2$ Fg.; L: $n*(n+1)/2$ Fg.
N ist D, N ist S, N ist A, D ist S, I ist S, I ist D, D ist R, D ist L.

Hilfsfunktionen zum Erzeugen von Matrizen

 

10-22 z.B. A = ones(5) - eye(5)

10-23 Di = diag(1:2:29)

10-24 n = 4; z = [ eye(n) eye(n) eye(n)]; B= [z ; z ; z]

10-25 Beispiel für n=3 im File 'magquadquad.m'

M=magic(3) ; MM= [];
for k=1:3
H = [ (M(k,1)-1)*9*ones(3)+M (M(k,2)-1)*9*ones(3)+M (M(k,3)-1)*9*ones(3)+M];
MM=[MM; H];
end

Logische Operatoren angewandt auf Matrizen

 

10-26 Si = S==0

10-27 E = zeros(7); E(6,3:6)=1; E(4,3:5)=1; E(2,3:6)=1; E(2:6,2)=1; N= E==0;

Multiplikation von Matrizen

 

10-28 1. Produkt: [13 12 11; 23 22 21; 33 32 31] ;
2. Produkt: [11 23 36; 21 43 66; 31 63 96]

10-29 Beispiel: R = [ 11*a+12*c, 11*b+12*d; 21*a+22*c, 21*b+22*d ]

10-30 Z*Z = [ 17 10; 15 22] ; D*D = [ 30 36 42; 66 81 96; 102 126 150]

10-31 a*u+b*w = 1 ; a*v+b*x = 0; c*u+d*w = 0 ; c*v+d*x = 1;
D = a*d-b*c ; u = d/D; v = -b/D; w = -c/D; x = a/D

10-32 legal; A+A, B+B, A+B, B*A', A*v, v*v', v'*v, B*v, A'*v, A'*A, A*A' B*B

10-33 legal: alle Produkte mit eigener Transponierten
illegal: alle Produkte mit eigner Originalmatrix
legal: E*S, S*E, E'*S', S'*E', Z*D, Z'*D', D*Z, D'*Z'

10-34 legal:w*A, A'*w', w*w', w'*w, v'*v, v*v',N*v, v'*N, A*N, A*N',

10-35 [a b ; c d] * [ d -b; -c a] = [ a*d-b*c, 0; 0, -c*b+d*a]

Formulieren von Gleichungssystemen in Matrizenform

 

10-36 M = [ 1 1 1 1; 1 -1 0 0; 0 -1 1 1; -1 0 1 0]
b= [0 1 -1 1]'; x=M $\backslash$b = [ 1 0 2 -3]'

10-37 M = [ 1 -2 0 0; 0 1 1 0; 1 0 0 -1; 1 -3 0 1] ; b = [ 0 5 2 1]

10-38 M = [ 1 -1 0 0; 0 1 -1 1; 0 0 1 -1; 1 0 0 1]
b= [5 3 1 3]'; x=M $\backslash$b = [ 9 4 -5 -6]'

10-39 M = [ 3 1 -1; 1 0 2; 0 1 -1]
b= [7 3 0]'; x=M $\backslash$b = [2.333 0.333 0.333 ]'

Einfache Funktionsplots

 

10-40 x=0:0.01:2 ; y1=x.^2; y2=y1.^2; y3=y2.^2; y4=y3.^2;
plot(x,y1,'r'); hold on; axis([0 2 0 2]) ; axis square;
plot(x,y2,'g'); plot(x,y3,'b'); plot(x,y4,'k');

10-41 x=-2:0.01:2 ; y1=x.^2; y2=x.^3; y3=x.^4; y4=x.^5;
plot(x,x,'r'); hold on; axis([-2 2 -2 2]) ; axis square;
plot(x,y1,'k'); plot(x,y2,'r'); plot(x,y3,'k'); plot(x,y4,'r');

10-42 x=0.01:0.01:4 ; y2=sqrt(x); y3=x..^(1/3); y4=x..^(1/4);
plot(x,x,'r'); hold on; axis([0 4 0 4]) ; axis square;
plot(x,y2,'g'); plot(x,y3,'b'); plot(x,y4,'k');

MATLAB-Operatoren und Grundfunktionen

 

10-43 Siehe Zusammenstellung der MATLAB-Operatoren

10-44 Zum Beispiel pi, eps

10-45 Zum Beispiel fliplr(flipud(M'))

Lösungen zu den Selbsttests

 

T111 - Punkt-Operatoren verlangen elementweise Verarbeitung,
es gibt sie für '*' '/' '\' '^' .
- eye(4)   - plot(x,y,'k')    - zei4=M(4,:)

T112 t = (0:0.01:3)*2*pi ; plot(t,sin(t)); axis equal

T113 Z=[1 0; 0 1]; V=[Z Z; Z Z] ; S=[V V; V V]

T114 p=-10:0.2:10; s=[p p p p p]

T115 M=[1 0 1; 0 1 1; 1 -2 -4]; b=[4 2 2]'; x=M\b

T121- xsol = A    - n frei wählbare Grössen auf der Diagonalen    - hold on
      -for zei=1:3 ; for spa=1:3; E3(zei,spa) =0; end;end;
zei = 1:3; E3(zei,zei) = 1; end; E3

T122 x=0.02:0.02:3; plot(x,x.^(1/2),x,x.^(1/3),x,x.^(1/4))

T123 load tempmess.dat; D=tempmess(:,2:4); plot(tempmess(:,1),D)

T124 for k=1:201; if y(k) > 0.6; y(k) = 0.6;
elseif y(k) < -0.6; y(k) = -0.6; end; end

T125 B*C= [4 13 1; 10 32 2; 0 10 0]