31-1 M= 5x5 tridiag(-1 2 -1), Det(M) = 6
31-2 n= 4,6,8,10; n! = 24, 720, 40320, 3628800
n^3= 64, 216, 512, 1000.
31-3 Ein Beispiel det(A)= -0.004091 [L,R,P]= lu(A), prod(diag(R)) = -0.004091
32-1 R= 10 Ohm, Rvar= 1..100 Ohm, C=50 pF, f = 200 MHz.
C=-j/(200e6*2*pi*0.05e-9);
R = 10
Rout = 1E6
for Rvar = 1:100
M = [1 -1 0 -1 0 0;0 1 -1 0 0 -1; 0 0 0 1 -1 1; ...
0 C 0 -R 0 Rout; 0 0 Rvar 0 -R -Rout; 0 C Rvar 0 0 0];
b=[0 0 0 0 0 1]';
cur= M\b;
cph(Rvar) = cur(6);
end
plot(angle(cph)*180/pi);
33-1
D=zeros(ndim); for k=1:ndim D(k,k)= k; end
33-2
W=zeros(ndim);
for zei=1:ndim
for spa=1:ndim
W(zei,spa)= 10*zei+spa;
end
end
33-3
L=zeros(ndim);
for zei=1:ndim
for spa=1:zei
L(zei,spa)= zei-spa+1;
end
end
33-4
R=zeros(ndim);
for zei=1:ndim
for spa=zei:ndim
R(zei,spa)= sqrt(zei^2+spa^2);
end
end
33-5
T=2*eye(ndim); for k=1:ndim-1 T(k,k+1)= -1; T(k+1,k)= -1; end
33-6
S=zeros(2*ndim); for k=1:2:2*ndim S(k:k+1,k:k+1)= [0 -1 ; 1 0]; end
30-1 v - w = [ 0 1 0]'; mit u = [0 1 0]'
wird also v-w-u=0.
die 2er Gruppen v,w ; w,u und v,u
sind aber linear unabhängig.
30-2 Die Differenz zwischen a und b ist [ 1 1 1 1]' mit x = [ 0 0 1 1]' werden a,b,c,x linear abhängig. Ob alle 3-er Gruppen dann linear unabhängig sind, muss noch geprüft werden, ist aber aus der Analogie zwischen c und x zu erwarten.
30-3 Es gilt b-c = d, also muss einer dieser drei Vektoren wegfallen. Alle Kombinationen, bei denen einer dieser Vektoren fehlt, haben Rang 4.
30-4 es gilt a-5*b = -c und d+e=a. Damit haben [a b c d], [a b c e], [a b d e], etc. alle Rang 3.
30-5 Mit a=0 werden die 1. und 2. Spalte identisch. Mit b=0.5 werden die 3. und 4. Spalte Vielfache voneinander. Somit ergibt a=0, b=0.5 Minimalrang 2. Mit a=1 und b=0 wird Rang=4 erreicht.
30-6 a) q=2, p=beliebig oder q 
und p=0 liefern Rang 2.
b) mit q=3 gilt unter den Spalten b+d=c. Mit p=-1 gilt zusätzlich b-d=a.
Beide Bedingungen gleichzeitig erfüllt, ergeben Minimalrang 2,
beide gleichzeitig verletzt ergeben Maximalrang 4.
30-7 a+b+c=11; 100*a+10*b+c - (100*c+10*b+a) = 594; 100*a+10*b+c - ( 100*a+10*c+b) = 18; M= [1 1 1; 99 0 -99; 0 9 -9] ; b=[ 11 594 18]'; z = [7 3 1]
30-8 a+b+c+d = 13; 1000*a+100*b+10*c+d - (1000*d+100*c+10*b+a) = 6264;
c=d; a-d=6;
M=[1 1 1 1; 999 90 -90 -999; 0 0 1 -1; 1 0 0 -1]; b=[13 6264 0 6]';
z=[7 4 1 1];
30-9 u2=1.5*u1+100; u3=1.5*u2+100; u4=1.5*u3+100; u5=1.5*u4+100;
u1+u2+u3+u4+u5=4000;
M=[-1.5 1 0 0 0; 0 -1.5 1 0 0; 0 0 -1.5 1 0; 0 0 0 -1.5 1; 1 1 1 1 1]
b = [ 100 100 100 100 4000]
u=[ 179.15 368.72 653.08 1079.62 1719.43]' kFr.
30-10 s2=s1*1.2+20; s3=s2*1.2+20; s4=s3*1.2+20; s5=s4*1.2+20; s1+s2+S3+S4+S5=1000; M=[-1.2 1 0 0 0; 0 -1.2 1 0 0; 0 0 -1.2 1 0; 0 0 0 -1.2 1; 1 1 1 1 1] b=[20 20 20 20 1000]' ; s= [ 101.57 141.88 190.26 248.31 317.97]' kFr.
30-11 A+B+C+D+E = 20; D= 10*(B-0.5); D = A+B+E; C-1= A+D+E; D-B = 2*A; M= [1 1 1 1 1; 0 -10 0 1 0; -1 -1 0 1 -1; -1 0 1 -1 -1; 2 1 0 -1 0] b = [20 -5 0 1 0]'; Br=[ 2 1 10 5 2];
30-12 Stand am Anfang des 4. Tages = 120-48-16=56 GLh. Zeitbedarf bei Leistung (2+2*0.8) = 1.6 : 15.56h Die Arbeit wird theoretisch (0.44h) 26 Minuten früher fertig.
30-13 Nacht: 12 h Zufluss mit G/12 pro Stunde.
7-8h (Pumpleistung x/h + Zufluss G/12/h)*1h = -G/6, also x=G*3/12/h
8-9h weiter wie 7-8 ergibt Füllstand G*2/3
9-t h Ab Füllstand 2/3 + ( Zufluss G/12 - 2*Pumpleistung G*3/12)*t = 0
t = 1.6 h, die Grube ist um 10h 36 leer (statt um 13 Uhr ohne 2. Pumpe)
30-14 G läuft mit der Geschwindigkeit 1U/h, k mit U/12/h.
Es gilt mit Start ab 12h (bzw. 0h) G*t = k*t + n, n= 1,2 ...11
(1-1/12)*t=n hat 11 Lösungen für n=1:11 nämlich
1.0909= 12/11, 2.1818=2*12/11 etc bis 11*12/11 =12h
30-15
M= [ 1 -1 0 -1 0 0 0 0 0 0 0; 0 1 -1 0 -1 0 0 0 0 0 0;
0 0 1 0 0 -1 0 0 0 0 0; 0 0 0 1 0 0 -1 0 -1 0 0;
0 0 0 0 1 0 1 -1 0 -1 0; 0 0 0 0 0 1 0 1 0 0 0;
0 0 0 0 0 0 0 0 0 1 1; 0 100 0 -200 100 0 -200 0 0 0 0;
0 0 250 0 -100 100 0 -100 0 0 0; 0 0 0 0 0 0 200 0 -100 50 -250;
0 0 0 200 0 0 0 0 100 0 0]
b=[ 0 0 0 0 0 0 0 0 0 0 10 ]'
cur = M\b*1000
%
%~[56.3 25.5 4.6 30.8 20.8 4.6 -7.6 -4.6 38.4 17.9 -17.9]'*0.001
30-16 Knoten 1,2,3 oben, 4 5 6 unten, i0 = Batt, i1 = 1-2, i2= 2-3, nach rechts
i3=1-4, i4=2-5, i5=3-6, nach unten, i6 = 4-5, i7 = 5-6
M= [ 1 -1 0 -1 0 0 0 0; 0 1 -1 0 -1 0 0 0 ; 0 0 1 0 0 -1 0 0; ...
0 0 0 1 0 0 -1 0; 0 0 0 0 1 0 1 -1; 0 100 0 -200 400 0 -100 0; ...
0 0 100 0 -400 1000 0 -500 ; 0 100 100 0 0 1000 0 0 ]
b=[ 0 0 0 0 0 0 0 -10 ]'
c= M=
[ 22.09 12.27 7.98 9.82 4.29 7.98 9.82 14.11 ]' *0.001
30-17 Nur obere Hälfte, Kirchhoff-Matrix
R=100
M= [ 1 -1 0 0 -1 0 0 0 0 0 0 0 0 0 ; ...
0 1 -1 0 0 -1 0 0 0 0 -1 0 0 0 ; ...
0 0 1 -1 0 0 -1 0 0 0 0 -1 0 0 ; ...
0 0 0 1 0 0 0 0 0 0 0 0 -1 0 ; ...
0 0 0 0 1 0 0 -1 0 0 1 0 0 0 ; ...
0 0 0 0 0 1 0 1 -1 -1 0 1 0 0 ; ...
0 0 0 0 0 0 1 0 1 0 0 0 1 -1 ; ...
%
0 R 0 0 -R 0 0 0 0 0 R 0 0 0 ; ...
0 0 R 0 0 -R 0 0 0 0 0 R 0 0 ; ...
0 0 0 R 0 0 -R 0 0 0 0 0 R 0 ; ...
0 0 0 0 0 R 0 -R 0 0 -R 0 0 0 ; ...
0 0 0 0 0 0 R 0 -R 0 0 -R 0 0 ; ...
0 0 0 0 0 0 0 0 R -R 0 0 0 R ; ...
R R R R 0 0 0 0 0 0 0 0 R R ]
b = [0 0 0 0 0 0 0 0 0 0 0 0 0 10]'
cur = M\b
% Loesung: Cur = [41.14 22.07 12.04 3.68 19.06 13.04 ...
% 7.36 16.05 6.35 23.75 -3.01 1.00 3.68 17.39 ]
% Ersatzwiderstand obere Haelfte 243.1 Ohm, symmetrich 121.5 Ohm
30-18
% ---Matlab-File--- wheatstone.m --------
% die Widerstaende R1, R2, R3, R4 und R5 muessen vor
% dem Ausfuehren dieses m-Files definiert werden,
% ein kleiner Wert von R5 erhoeht die Empfindlichkeit.
M =[ 1 -1 0 -1 0 0 ;
0 1 -1 0 0 -1 ;
0 0 0 1 -1 1 ;
0 R1 0 -R3 0 R5 ;
0 0 R2 0 -R4 -R5 ;
0 R1 R2 0 0 0 ] ;
b = [ 0 0 0 0 0 10 ]' ;
isol = M \ b;
% Das hauptsaechlich interessierende Resultat ist
% der Strom in der Bruecken-Strecke R5
tx = 'Strom in Brueckenzweig:' ;
tx i5 = isol(6) ; i5
% -- end --- wheatstone.m ---------
30-19 Quadrat 2x2 obere Hälfte 3k
,
total 1.5k
Quadrat 3x3 obere Hälfte 3.71k
,
total 1.86k
Quadrat 4x4 ,
total 2.14k
30-20
function icplx=seriereso(freq)
w = 2*pi*freq;
C = -j/0.3e-6/w;
L = j*w*2e-4;
R = 10;
ct = 1/(R+C+L);
icplx = R*ct;
30-21
function ivec=resonet(freq)
w = 2*pi*freq;
C = -j/100.0e-9/w;
L = j*w*10e-4;
R = 10;
Rv = 30;
M = [ 1 -1 -1 0 0; 0 1 0 -1 0; 0 0 1 0 -1; 0 R -C L 0; 0 0 C 0 Rv];
b = [0 0 0 0 10]';
ivec = M\b;
30-22
Up = 10; Ua = Up/2; w=2*pi*10000; for k=1:40 cb = Up/(k*50-j/(w*50e-9)); Ub = Up - cb*k*50; dU(k) = Ua-Ub; end plot(angle(dU)*180/pi)
30-23
R=zeros(n);
for zei= 1:n
for spa = zei:n
R(zei,spa) = 1;
end
end
30-24
H=zeros(2*n)
spa= 1
for zei= 1:n
H(zei,spa) = 1;
spa = spa+2;
end
spa = 2
for zei= n+1:2*n
H(zei,spa) = 1;
spa = spa +2
end
30-25
T=zeros(n);
for zei= 1:n
T(zei,zei) = 2;
end
for zei= 1:n-1
T(zei,zei+1) = -1;
T(zei+1,zei) = -1;
end
30-27
C=zeros(n)
for zei= 1:n
for spa = 1:n
C(zei,spa) = zei + j*spa
end
end
30-28
S=zeros(n);
for zei= 2:2:n
for spa = 1:2:n
S(zei-1,spa) = 1;
end
for spa = 2:2:n
S(zei,spa) = 1;
end
end
if zei < n
for spa = 1:2:n
S(n,spa) = 1;
end
end
S
30-29
C=zeros(n);
for zei= 1:n
for spa = 1:zei
C(zei,spa) = zei + spa;
end
end
30-30 Siehe universell anwendbare M-Files.
30-31 Ein Beispiel x.^3:
fuction retvec = pow3(x) % retvec = pow3(x) berechnet Elementweise x ^ 3 retvec = x.^3;
30-32
function iforth = orthotest(Q)
[n,m]=size(Q);
if n==m
if max(max(abs(Q.'*Q -eye(n))) ) < 1e-14
iforth = 1;
else
iforth = 0;
end
else
iforth=0;
end
30-33
function Mtra = selftransp(Mori)
[n,m]=size(Mori);
if n == m
for zei = 2:n
for spa = 1:zei-1
h = Mori(zei,spa);
Mori(zei,spa) = Mori(spa,zei);
Mori(spa,zei) = h;
end
end
Mtra = Mori;
else
Mtra = [];
end
30-34 Einfach ausprobieren, selektiert eine Zeile/Spalte platziert diese in eine andere, falls die Eins nicht auf der Diagonalen steht.
30-35 Einzig jeweils
T(1,1)=1, T(2,1)=1, T(4,1)=1, T(5,1)=1;
T(1,4)=1, T(2,4)=1, etc. T(5,5)=1 und T(k,h)=0 für alle anderen.
30-36 Einzig jeweils
T(1,1)=1, T(1,2)=1, T(1,4)=1, T(1,5)=1;
T(4,1)=1, T(4,2)=1, etc. T(5,5)=1 und T(k,h)=0 für alle anderen.
30-37 Ausprobieren! Achtung - dies stimmt nur für echte Permutationsmatrizen (vollständige Turmmatrizen)! Alle Spechtmatrizen und unvollständigen Turmmatrizen, hier als Auswahlmatrizen bezeichnet werden, sind singulär und damit nicht orthogonal!
30-38 Für einfache Vertauschungen gilt bereits
, für scroll-up scroll-down erst 
.
30-39
function rper = rndperm(n) % Erzeuge eine Turmmatrix Dim n % mit zufaelliger Permutation % der Laenge des Eingabevektors rper = zeros(n); % in jede Zeile kommt eine Eins % an einen noch freien Platz nfr = n; indfree = 1:n; for zei = 1:n-1 rz = rand(1)*nfr; irz = fix(rz) + 1; rper(zei,indfree(irz))= 1; % der Vektor der freien Plaetze wird verkuerzt indfree(irz) = []; nfr = nfr-1 end rper(n,indfree(1))= 1;
30-40
function tubk = makturm(pv) % makturm Erzeuge eine Turmmatrix zum % gegebenen Permutationsvektor nd = length(pv); % Rueckgabematrix quadratisch mit Dimension % der Laenge des Eingabevektors tubk = zeros(nd); % in jede Zeile kommt in diejenige Spalte % die als Zahl in pv steht eine Eins for zei = 1:nd tubk(zei,pv(zei))= 1; end
30-41 Nur die zyklischen Versionen haben Rang 5, die anderen Rang 4
Sue = [0 1 0 0 0; 0 0 1 0 0; 0 0 0 1 0; 0 0 0 0 1; 0 0 0 0 0]
Suz = [0 1 0 0 0; 0 0 1 0 0; 0 0 0 1 0; 0 0 0 0 1; 1 0 0 0 0]
Sde = [0 0 0 0 0; 1 0 0 0 0; 0 1 0 0 0; 0 0 1 0 0; 0 0 0 1 0]
Sdz = [0 0 0 0 1; 1 0 0 0 0; 0 1 0 0 0; 0 0 1 0 0; 0 0 0 1 0]
30-42 Von links her wirken Scroll-up/down Matrizen wie erwartet. Bei Multiplikation von rechts wirken sie für die Spalten als scroll-right bzw. scroll-left Matrizen.
30-43 Pl = [0 0 0 0; 1 0 0 0; 0 0 0 1; 0 0 0 0] Pr = [0 0 0 1; 0 0 1 0; 0 1 0 0; 1 0 0 0]
30-44
B14 = [0 0 0 1; 0 1 0 0; 0 0 1 0; 1 0 0 0]
B23 = [1 0 0 0; 0 0 1 0; 0 1 0 0; 0 0 0 1]
P4321 = B14*B23
B14^2
30-45
Tl = [0 0 0 1; 0 0 1 0; 0 1 0 0; 1 0 0 0]
Tr = [0 0 0 1; 0 0 1 0; 0 1 0 0; 1 0 0 0]
30-46 Für 
gilt
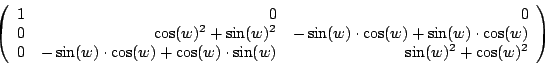
30-47 Benutzen Sie die Möglichkeit zum Eingeben einer von Ihnen gewählten Matrix! Als Spezialbeispiel kann eine bereits in Dreiecksform vorliegende Matrix eingegeben werden.
30-48
% code Fragment Verarbeitung von A steht bei Spalte 'k' xmx = A(k,k); pzei = 0; for ze = (k+1):ndim if A(ze,k) > xmx pzei = ze; xmx = A(ze,k); end end if pzei > 0 H = A(k,k:ndim); A(k,k:ndim) = A(pzei,k:ndim) A(pzei,k:ndim) = H end
30-49
function xsol = trirbksub(T,b) [m,n]= size(T); xsol(n) = b(n)/T(n,n); for k = (n-1):(-1):1 x(k) = (b(k) -x(k+1)*T(k,k+1); end
30-50
A=[4 4 8; ;2 -3 4 ; 1 2 1] L1 = [1 0 0; -1/2 1 0; -1/4 0 1] L1I = [1 0 0; 1/2 1 0; 1/4 0 1] L1*A L2 = [1 0 0; 0 1 0; 0 1/5 1] L2I = [1 0 0; 0 1 0; 0 -1/5 1] L2*L1*A [LL,RR,P]= lu(A) LI = L1I*L2I
30-51
C = [ 1 0 0; -3/2 1 0; -5/2 0 1] M = [ 2 3 4; 3 1 1 ; 5 0 1] C*M
30-52
RR=[1 2 3 ; 0 4 5; 0 0 6] L1 = [1 0 0; 0.5 1 0; -1 0 1] L1I = [1 0 0; -0.5 1 0; 1 0 1] L2 = [1 0 0; 0 1 0; 0 -0.4 1] L2I = [1 0 0; 0 1 0; 0 0.4 1] L1I*L2I*RR [L R P ] = lu(ans)
30-53
A = [4 8 4; 2 2 4; 1 3 -1 ] [L R P] = lu(A); L\eye(3) x = R\y y = [1 0 0; -1/2 1 0; -1/2 1/2 1] x = [-7/4 5/2 3; 3/4 -1 -1; 1/2 -1/2 -1] Ainv = [-1.75 2.5 3; 0.75 -1 -1; 0.5 -0.5 -1]
T311 - 4 - Man setzt den Koeffizienten
dieses Vektors Null und erhält den Nullvektor mit
Koeffizienten die nicht alle Null sind.
- 0 - Durch Rückwärts-Einsetzen
T312 Es=ones(n);
for zei=1:n-1;for spa=zei+1:n; Es(zei,spa)=0;Es(spa,zei)=0; end;end
T313 I=eye(6);I(1,1)=0;I(3,3)=0;I(5,5)=0
Pa=I; Pa(3,1)=1; Pa(5,3)=1; Pa(1,5)=1;
Pb=I; Pb(5,1)=1; Pb(3,3)=1; Pb(1,5)=1;
T314
% w=angofvect(w,v) Winkel zwischen zwei Vektoren function angval = angofvect(v,w) angval = acos( v'*w/sqrt((v'*v)*(w'*w)) )*180/pi;
T315 b=[0 0 2 1 0]'
M=[1 -1 1 -1 1; 0 0 0 0 0; 16 8 4 2 1; 1 1 1 1 1; 4 3 2 1 0]
x=M\b
T321 - b=0 setzen
- Bildraum aufgespannt
durch [1 0 0]' und [0 0 1]', Nullraum: [0 p p]'
- Turmmatrix:n, Spechtmatrix: 1 - orthogonal
T322 T=2*eye(n)
for spa=3:n;T(spa-2,spa)=-1;T(spa,spa-2)=-1; end
T323
% iasymm = asymmtest(A) testet asymmetrie (=1) sonst (0) function iasymm = asymmtest(A) [nn,n]=size(A); iasymm = 1; for zei = 1:n; for spa=zei:n; if A(spa,zei) ~= -A(zei,spa); iasymm = 0; break; end; end; end;
T324 Px=[1 0 0; 0 0 0; 0 0 0]
Py=[0 0 0; 0 1 0; 0 0 0] Pz=[0 0 0; 0 0 0; 0 0 1]
Rang 1
T325n=length(v); s = 0
for k=1:n; s=s+v(k)^2; end; vecnor = sqrt(s)