b)]
c)
d)]
60-1
% halbkugelkontur.m
z=zeros(41);
for zei = 1:41
for spa = 1:41
y(zei) = (zei-21)*0.05;
x(spa) = (spa-21)*0.05;
if x(spa)^2+y(zei)^2 < 1
z(zei,spa)= sqrt(1-x(spa)^2-y(zei)^2);
end
end
end
contour(x,y,z,25) ; axis([-1 1 -1 1]); axis square; pause
contour3(x,y,z) ; axis equal; pause
surf(x,y,z) ; axis equal;
60-2
% sincoskontur.m
z=zeros(41);
for zei = 1:41
for spa = 1:41
y(zei) = (zei-1)*0.05*pi;
x(spa) = (spa-1)*0.05*pi;
z(zei,spa)= sin(x(spa))*cos(y(zei));
end
end
contour(x,y,z,25) ; axis([0 6.3 0 6.3]); axis square; hold on
xstat = [0.5 1.5 0.5 1.5 0.5 1.5 0 1 2 0 1 2]*pi;
ystat = [ 0 0 1 1 2 2 0.5 0.5 0.5 1.5 1.5 1.5]*pi;
plot(xstat,ystat,'or'); hold off; pause
contour3(x,y,z,20) ; axis equal; pause
surf(x,y,z) ; axis equal;
60-3
% jurakontur.m
z=zeros(41);
for zei = 1:41
for spa = 1:81
y(zei) = (zei-21)*40;
x(spa) = (spa-41)*80;
z(zei,spa)= max(1100,1600 -x(spa)^2/20000 - y(zei)^2/1250);
end
end
contour(x,y,z,15) ; axis equal;
pause
contour3(x,y,z,20) ; axis equal; pause
surf(x,y,z) ; axis equal;
60-4
% specmatkontur.m
z=indmatf(9); contour(z); pause
Du = zeros(21);
for zei = 1:21
for spa = zei:41
Du(zei,spa)= spa-zei;
end
end
Ph = [ Du fliplr(Du) ]; P = [ flipud(Ph) ; Ph ];surf(P)
axis equal ; view(-20,62)
60-5
% dumatkontur.m surf(Du); pause; surf(Du^2); pause; surf(Du.^2); pause C = fliplr(Du); surf(C.^3); pause; surf(C^3); pause; surf(C*Du)
60-6
% trichterkontur.m
z=zeros(85);
for zei = 1:85
for spa = 1:85
y(zei) = (zei-43)*0.5;
x(spa) = (spa-43)*0.5;
if x(spa)^2+y(zei)^2 <= 21^2
z(zei,spa)= sqrt(x(spa)^2+y(zei)^2)-0.5;
end
end
end
contour(x,y,z,25) ; axis([-22 22 -22 22]); axis square; pause
contour3(x,y,z,20) ; axis equal; pause
surf(x,y,z) ; axis equal;
60-7
% kissenkontur.m
z=zeros(41,61);
for zei = 1:41
for spa = 1:71
y(zei) = (zei-21)*0.05;
x(spa) = (spa-36)*0.05;
z(zei,spa)= 0.4* (1-(x(spa)*4/7)^8)*(1-y(zei)^4);
end
end
contour(x,y,z,15) ; axis equal; pause
contour3(x,y,z,20) ; axis equal; pause
surf(x,y,z) ; axis equal ; colormap(winter)
60-8 siehe Beispiel-M-File.
60-9
a)
![]() ,
,
![]() ,
,
![]()
b)]
![]() ,
,
![]()
c)
![]()
![]()
d)]
![]() ,
,
![]()
![]()
![]()
60-10
a)
![]()
![]()
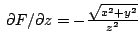
b)
![]()
![]()
c)
![]()
![]()
![]()
60-11
syms x y z f1 = x^2+y^2 ; pdx1 = diff(f1,x); pdy1 = diff(f1,y) %pdx1,pdy1 = 2*x , 2*y f2 = sin(x)*cos(y); pdx2 = diff(f2,x); pdy2 = diff(f2,y) %pdx2,pdy2 = cos(x)*cos(y); -sin(x)*sin(y); f3 = 1/sqrt(x^2+y^2+z^2); pdx3 = diff(f3,x); pdy3 = diff(f3,y); pdz3 = diff(f3,y)y3 = diff(f3,y) %pdx3, pdy3 = -x/(sqrt(x^2+y^2+z^2))^3, -y/(sqrt(x^2+y^2+z^2))^3 % pdz3 = -z/(sqrt(x^2+y^2+z^2))^3
60-12
%sincontgrad.m Konturplot mit eingezeichnetem Gradient [X,Y] = meshgrid([0:.1:1]); Z = sin(pi*X).*sin(pi*Y); contour3(X,Y,Z,30) figure(2); clf [px,py] = gradient(Z,.2,.2); contour(X,Y,Z) ; hold on quiver(X,Y,px,py) % malt Pfeile axis equal ; hold off
60-13
%jhillcontgrad.m Konturplot mit eingezeichnetem Gradient [X,Y] = meshgrid([-1600:50:1600],[-400:50:400]); Z = max(1600 -(X/1000).^2*50 -(Y/250).^2*50,1400) ; contour3(X,Y,Z,20); axis equal figure(2); clf [px,py] = gradient(Z,50,50); %Abst\"ande zwischen Punkten subplot(3,1,1) contour(X,Y,Z,15) ; hold on % Ausduennen der gezeichneten Pfeile xsel = 1:4:65; ysel=1:2:17; Xs = X(ysel,xsel);Ys = Y(ysel,xsel); pxs = px(ysel,xsel) ; pys = py(ysel,xsel); quiver(Xs,Ys,pxs,pys) % erstellt Pfeile axis equal ; subplot(3,1,2); contour(X,Y,px,15) subplot(3,1,3); contour(X,Y,py,15) hold off
60-14 Die Funktions-M-Files können im allgemeinen Programm divfctcont() eingesetzt werden.
%z=minihillf(Xgr,Ygr) Funktion zur Definition der Flaeche % 1 - x^2 - 0.2*y^2 function z=minihillf(Xgr,Ygr) z = 1 - Xgr.^2 - 0.2*Ygr.^2 ;
%z=sinsinf(Xgr,Ygr) Funktion zur Definition der Flaeche % sin(pi*x) * sin(pi*y) function z=sinsinf(Xgr,Ygr) z = sin(pi*Xgr).*sin(pi*Ygr);
%z=pwdiff(Xgr,Ygr) Funktion zur Definition der Flaeche % (x^2 - abs(x^3)) * (y^2 - abs(y^3)) function z=pwdiff(Xgr,Ygr) z =(Xgr.^2 - abs(Xgr.^3)) .* (Ygr.^2 - abs(Ygr.^3)) ;
function plhd = divfctcont(fctnam,xvec,yvec) % plhd = divfctcont(fctnam,Xgrid,Ygrid) % Konturplot von mit 'fctnam' waehlbarer Funktion [X,Y] = meshgrid(xvec,yvec); Z = feval(fctnam,X,Y); figure(1); clf contour3(X,Y,Z,30) figure(2); clf [px,py] = gradient(Z,xvec,yvec); plhd = contour(X,Y,Z,25) ; hold on quiver(X,Y,px,py) %erstellt Pfeile axis equal ; hold off
60-15
% p2p4findstat.m - Symbolic script sucht Stationaere Punkte
syms xs ys
fs = (xs^2-xs^4)*(ys^2-ys^4)
dfx = diff(fs,xs)
dfy = diff(fs,ys)
stptsol = solve(dfx,dfy)
stptsol.xs
stptsol.ys
%{xs 0} {0 ys}{+-1 +-1} {+-\sqrt(2)/2 +-\sqrt(2)/2}
%p2p4stat.m Konturplot mit stationaeren Punkten [X,Y] = meshgrid([-1.1:0.1:1.1]); Z = 10*(X.^2-X.^4).*(Y.^2-Y.^4) ; figure(1); clf contour3(X,Y,Z,20); axis equal figure(2); clf contour(X,Y,Z,15) ;
60-16 Mit der Funktion
%z=biquartf(Xgr,Ygr) Funktion zur Definition der Flaeche
% 0.25x^4-0.5x^2 + 0.25y^4-0.5y^2 -0.12x -0.05y + 1
function z=biquartf(Xgr,Ygr)
z=(0.25*Xgr.^4-0.5*Xgr.^2)-0.12*Xgr ...
+(0.25*Ygr.^4-0.5*Ygr.^2)+1-0.05*Ygr;
ergibt sich der Aufruf ganz einfach als:
divfctcont('biquartf',-1.7:0.2:1.7, -1.7:0.2:1.7)
60-17 Die Funktion
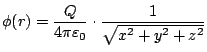 hat die drei partiellen Ableitungen
hat die drei partiellen Ableitungen
![]() damit ist
damit ist
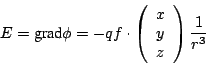
60-18
x = 0:4 ; y = [1 1.2 2.2 3 3.6];
M1 = [sum(x.^2) sum(x); sum(x) 5]; b1 =[ sum(x.*y) ; sum(y)];
M2 = [sum(x.^4) sum(x.^3) sum(x.^2); sum(x.^3) sum(x.^2) sum(x); ...
sum(x.^2) sum(x) 5];
b2 =[ sum(x.^2.*y) ; sum(x.*y) ; sum(y)];
M3 = [sum(x.^6) sum(x.^5) sum(x.^4) sum(x.^3);...
sum(x.^5) sum(x.^4) sum(x.^3) sum(x.^2);
sum(x.^4) sum(x.^3) sum(x.^2) sum(x);
sum(x.^3) sum(x.^2) sum(x) 5 ];
b3 =[ sum(x.^3.*y); sum(x.^2.*y) ; sum(x.*y) ; sum(y)];
p1 = M1\b1
p2 = M2\b2
p3 = M3\b3
60-19
x = [-3 -2 -1 0 1 2 3]'; A=[x.^3 x.^2 x [1 1 1 1 1 1 1]']; b = [-7 -5 -2 0 -1 2 0]'; p=A\b
60-20
x = (-2:2)' ; y = [-2 0 1 1.5 3]'; w = [4 2 1 2 4]'; Mn = [sum(x.^2) sum(x); sum(x) 5]; bn =[ sum(x.*y) ; sum(y)]; A = [x ones(5,1)]; pn = Mn\bn ; pf = A\y; Aw = A.*[w w]; yw = y.*w; pfw = Aw\yw; Mw = [sum(w.^2.*x.^2) sum(x.*w.^2); sum(x.*w.^2) sum(w.^2)]; bw =[ sum(w.^2.*x.*y) ; sum(w.^2.*y)]; pnw = Mw\bw; pn, pf, pnw, pfw
60-21 Mit Matrizen von 6-20: A'*A-Mn A'*y-bn Aw'*Aw-Mw Aw'*y-bw
60-22 Mit den Bibliotheksfunktionen:
x = (1:5)' ; y = [1 3 4 2 1]'; p2 = polyfit(x,y,2) ; p3 = polyfit(x,y,3) xf = 0:0.05:6; y2 = polyval(p2,xf); y3 = polyval(p3,xf); plot(x,y,'or'); hold on; plot(xf,y2); plot(xf,y3,'g')
60-23
x = (0:0.2:1)'*pi ; y = sin(x);
varfctfit(x,y,'pow0fct','pow1fct','pow2fct')
% pkoef = varfctfit(x,y,'f1','f2', ...)
% linearer Fit nach einer variablen Anzahl Funktionen fk
function pkoef = varfctfit(varargin)
A=[];
for nf = 3:nargin
A=[A feval(varargin{nf},varargin{1})];
end
pkoef = A\varargin{2};
60-24
x = (0:0.1:0.9)' ; y = [0 1 1.2 0 1 0 0 0 0 -1]'; varfctfit(x,y,'sintpif') varfctfit(x,y,'sintpif','sin2tpif') varfctfit(x,y,'sintpif','sin2tpif','sin4tpif')
60-25
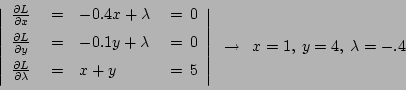
60-26
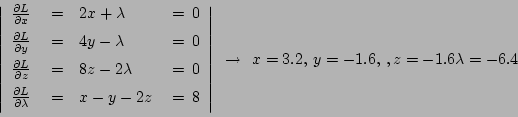
60-27
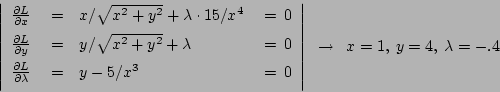
60-28
% hillagrange.m Figur zu Optimierung mit Nebenbedingung xv = -6:0.1:6; [xg,yg]=meshgrid(xv); H = 10 - 0.02*xg.^2 - 0.1*yg.^2; H = H .* (yg > xg-4) ; H=max(H,9); figure(1) ; clf; surf(xg,yg,H); view(15.5,11) figure(2) ; clf contour3(xg,yg,H) ; hold on LM = [-0.04 0 1 ; 0 -0.2 1 ; 1 -1 0]; Lb = [ 0 0 4]'; p= LM\Lb xel = 0:0.1:6; yel = -4+xel; zel = 10 - 0.02*xel.^2 - 0.1*yel.^2; zel = max(zel,9); plot3(xel,yel,zel,'k') view(15.5,18.0) ; hold off
60-29
x=(-3:3)'; A=[x.^3 x.^2 x x.^0]; y1 = [-1 1 1 0 0 1 3]'; y2 = [1 2 1 2 3 3 5]'; % Aufruf der Singular Value Decomposition [U , S , V] = svd(A); Si = S % nur S muss elementweise invertiert werden for k=1:4 Si(k,k) = 1/S(k,k); end Si % U und V sind orthogonal: U'*U=I Api= V*Si'*U'; p1 = A\y1 pp1 = Api*y1 p2 = A\y2 pp2 = Api*y2
60-30
![]()
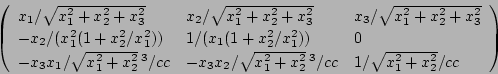
60-31
x= [5 5]'; fct2p2p4iter; fct2p2p4iter; fct2p2p4iter; % fct2p2p4iter.m - run Jacobi-Iteration fvec= fct2p2p4(x(1),x(2)) delx = fct2p2p4jac(x(1),x(2))\ fct2p2p4(x(1),x(2)) x = x-delx % fvec = fct2p2p4(x,y) Funktion zur jacobi-Iteration function fvec = fct2p2p4(x,y) fvec = zeros(2,1); fvec(1) = (x-4)^2+ y^2 -10; fvec(2) = x^4+ y^4 -20; %jac = fct2p2p4jac(x,y) Evaluation der Jacobi-Matrix function jac = fct2p2p4jac(x,y) jac = zeros(2); jac(1,1) = 2*x-8; jac(1,2) = 2*y; jac(2,1) = 4*x^3; jac(2,2) = 4*y^3;
60-32, 33 Siehe M-File-Sammlung.
T611 - Senkrecht zum Gradientenvektor, also
![]()
-
![]()
- Nur so wird die Nebenbedingung
als
![]() ein Teil des Gleichungssystems.
ein Teil des Gleichungssystems.
-
![]()
T612
[X,Y]=meshgrid(-1:0.02:1); h=max(1-X.^2-Y.^2,0); h=h.^2; contour3(X,Y,h,25); axis equal
T613
hA=0; hB=1; hC=4; hD=1; [X,Y]=meshgrid(0:0.1:5); h=hA + (hB-hA)*X/5 + (hD-hA)*Y/5 + (hC+hA-hD-hB)*Y.*X/25; contour3(X,Y,h,25); axis equal; box on; pause [gx,gy] = gradient(h,0.1,0.1); contour(X,Y,gx); pause contour(X,Y,gy);
T614
![\begin{displaymath}
\left\vert
\begin{array}{lclc}
\frac{\partial L}{\partial x...
...}
& ~=~& x+2y+4z -8
& ~=~ 0\\ [0.5em]
\end{array}\right\vert
\end{displaymath}](img729.png)
M=[8 0 0 1; 0 2 0 0; 0 0 0 4; 1 2 4 0]; b=[0 0 -1 8];
x = [0.312 0.25 1.8672 -0.25]'
T615
% newtexa als Funtion damit f und jac intern sind function xf = newtexa(xi,yi) xv=[xi;yi]; for k=1:8; xv = xv-newtexajac(xv)\newtexafct(xv); end; xf=xv; % fvec = newtexafct(xv) Beispielfunktion 2D Newton function fvec = newtexafct(xv) fvec = zeros(2,1); fvec(1) = xv(1)^4+xv(2)^4-20; fvec(2) = xv(1)^2 -xv(2)^2 -1; % newtexajac(xv) Beispielfunktion jac zu 2D Newton function jac = newtexajac(xv) jac(1,1)=4*xv(1)^3 ; jac(1,2)=4*xv(2)^3 ; jac(2,1)=2*xv(1) ; jac(2,2)=-2*xv(2) ;