next up previous contents
Nächste Seite: Lösungshinweise zum Kapitel 8 Aufwärts: Lösungshinweise Vorherige Seite: Lösungshinweise zum Kapitel 6   Inhalt


Lösungshinweise zum Kapitel 7

Numerische Lösung von Differentialgleichungen

 

70-1 

% wegweiser(xmx,ymx,f) zeichnet ein Wegweiserfeld zu y'=-f*y
%   mit Pfeilen an den Positionen 0:xmx 0:ymx
function voidbk = wegweiser(xmx,ymx,f)
hold on
for x=0:1:xmx
  for y=0:1:ymx
    w=atan(f*y);   putarrow(x,y,w);
  end
end
hold off
% internal function
function voidbk = putarrow(xpos,ypos,win)
xars = [0.08 0.25 -0.25 0.25 0.08; ...
         0.01  0     0     0    -0.01 ; 1 1 1 1 1];
xpl= [cos(win) -sin(win) xpos; sin(win) cos(win) ypos; 0 0 1]*xars;
plot(xpl(1,:),xpl(2,:))
for x=0:1:25
  for y=0:1:18
    w=atan(-0.1*y);     putarrow(x,y,w);
  end
end

70-2 $ dy/dt = -0.2 \cdot y ~$separieren$ ~ dy/y= -0.2 dt ~$integrieren$ ~ \ln(y) = -0.2 t+C $
$ y(x) = y(0)\cdot \mathrm{e}^{-0.2t}$ 

% simpdecay(f) L\"osung der simplen Dgl. y'=-f*y
yin = 15;  
[tsol,ysol] = ode45('simpdecayeval',25, yin);
plot(tsol,ysol);

% deri= simpdecayeval(tval,yval) die Ableitung y'=-0.2*y 
function deri  = simpdecayeval(tval,yval); 
deri = -0.2* yval;

70-3 

% selfeulerdecay  - ausprogrammiertes Euler-Verfahren
%   fuer Zerfallsgleichung  y'=-0.1*y
ttot = 50;  yin = 20;  lam = -0.1;
h = ttot/1000;  tsol = [0:1000]'*h;
ysol= zeros(1001,1);
%init
ysol(1) = yin;
%loop
for k=2:1001
  ysol(k) = ysol(k-1) + h* (lam*ysol(k-1));
end

70-4 

  yvec0 dyvec0  yvec1 dyvec1   yvec2   dyvec2   yvec3 
 x  10   0       10    -0.02    9.996  -0.04     9.988
 u   0  -0.1     -0.02 -0.1    -0.04   -0.1     -0.06
 y   0   1        0.2   1       0.4    0.9996   0.5999
 v   1   0        1   -0.002   0.9996  -0.004   0.9988
 t = 0           0.2            0.4             0.6

70-5 

% [tsol,ysol]= selfeuler(fctnam, ttot, yin)
%  ausprogrammierter ode-solver nach  Euler
%  mit gleicher signatur wie ode45()
function [tsol,ysol]= selfeuler(fctnam, ttot, yin)
h = ttot/1000;  tsol = [0:1000]'*h;
ysol= zeros(1001,length(yin));
%init
ysol(1,:) = yin';
%loop
for k=2:1001
  ysol(k,:) = ysol(k-1,:) +...
      h* ( feval(fctnam, (k-1)*h , ysol(k-1,:)') )';
end

Differentialgleichungen höherer Ordnung

 

70-6 

% deriv = dmposc(t,yac) Beispiel gedaempfter Oszillator
function deriv = dmposc(t,yac)
w = 1.08;
d = 0.01;
deriv = zeros(2,1);
deriv(1) = yac(2);
deriv(2) = -d*yac(2) -w*w*yac(1) + 0.2*sin(t) ;

% Skript rundmposc Integrieren und Zeichnen
yin = [0 0]';
[tsol, ysol] = ode45('dmposc', 200 , yin);
figure(1); clf
plot(tsol,ysol(:,1))
figure(2); clf
plot(tsol,ysol(:,2),'r')

70-7 

% haronmosc einfacher harmonischer Oszillator
function deri = harmonosc(tac,yac)
deri = zeros(2,1); deri(1) = yac(2) ; deri(2) = -yac(1);
% dmposc501  Beispiel gedaempfter Oszillator
function deri = dmposc501(tac,yac)
deri = zeros(2,1); deri(1) = yac(2) ; 
deri(2) = -25*yac(1) -0.1*deri(1); 
% splinederiv Ableitung der Spline-Bedingung y(IV) = 0
function deri = splinederiv(tac,yac)
deri = zeros(4,1); deri(1) = yac(2) ; 
deri(2) = yac(3); deri(3) = yac(4) ; deri(4) = 0;

70-8 

% runluftfall  - freier Fall mit Luftwiderstand
%   vorgaengig CLUFTBREMS definieren (0.5 - 0.001)
global CLUFTBREMS
[tsol,ysol] = ode45('luftfallderi',100,[0,0]);
figure(1); clf; plot(tsol,ysol(:,1)) 
figure(2); clf; plot(tsol,ysol(:,2)); figure(1) 

% deri = luftfallderi(tac,yac) Ableitung Fall in Luft 
function deri = luftfallderi(tac,yac)
global CLUFTBREMS
deri = zeros(2,1);
deri(1)=yac(2);
deri(2)=-9.81 + CLUFTBREMS*(yac(2))^2;

70-9 Siehe Beispiel-M-files

Systeme von Differentialgleichungen

 

70-10 Siehe Beispiel-M-files

70-11 

% runtochzerfpar zeigt Zeitfunktionen eines radioaktiven
%   Zerfalls mit Tochterkern
%   globale Parameter: LAMBDA1  LAMBDA2 interaqktiv abgefragt
global LAMBDA1;   global LAMBDA2
  LAMBDA1 = input('lambda1 eingeben');
  LAMBDA2 = input('lambda2 eingeben');
yin = [10 0]'
[xsol, ysol] = ode45('tochzerfpar', 50 , yin);
plot(xsol,ysol)

% deri = tochzerfpar(t,y) Ableitungen zum RA-Tochterzerfall
function deri = tochzerfpar(t,y)
global LAMBDA1 ; global LAMBDA2
deri = zeros(2,1);
deri(1) = -LAMBDA1*y(1); deri(2) = LAMBDA1*y(1) - LAMBDA2*y(2);

70-12 

% runchargpart.m
ystart=[ 0 0 0 1]';
[t45,y45]= ode45('chargpartderi',200,ystart);
plot(y45(:,1),y45(:,3),'r')

% deriv = chargpartderi(t,yac) Ableitung Teilchen 2D
%   in konstantem Magnetfeld
function deriv = chargpartderi(t,yac)
B=-1/10;  deriv = zeros(4,1);
deriv(1) = yac(2);  deriv(2) =  yac(4)*B ;
deriv(3) = yac(4);  deriv(4) = -yac(2)*B ;

70-13, 14, 15 siehe M-File Sammlung

Spline-Funktionen

 

70-16
a) $ y^{IV} = 0 $ hat die allgemeine Lösung $ f(x) =ax^3+bx^2+cx+d$. Die 4 Bedingungen an den beiden Rändern legen $ f(0)$, $ f(1)$, $ f'(0)$ und $ f'(1)$ fest. Das Gleichungssystem

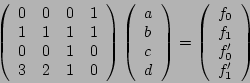
\begin{displaymath}\left( \begin{array}{llll} 0& 0& 0& 1\\ 1&1&1&1\\ 0&0&1&0\\... ...begin{array}{l} f_0 \\ f_1 \\ f_0' \\ f_1' \end{array}\right) \end{displaymath}

liefert $ d=f_0$,  $ c=f_0'$,  $ b =-3f_0 +3f_1 - 2f_0' -f_1'$,  $ a =2f_0 -2f_1 +f_0' +f_1'$
Dies ergibt für das Beispiel: $ f(x)=-0.6x^3+0.3x^2+0.5x+1$
b) Daraus ergeben sich die 4 elementaren Splinefunktionen zu $ f_0=1$: $ 2x^3-3x^2+1$,  zu $ f_1=1$: $ -2x^3+3x^2$,  zu $ f_0'=1$: $ x^3-2x^2+x$,  zu $ f_1'=1$: $ x^3-x^2$.

70-17
Die 4 Elementar-Splines sind:
B1: $ 2t^3-3t^2+1 = (2t+1)\cdot (t-1)^2$ Doppelte Nullstelle bei 1
B2: $ -2t^3+3t^2 = t^2 \cdot (3-2t)$ Doppelte Nullstelle bei 0
B3: $ t^3-2t^2+t = t\cdot (t-1)^2$ Doppelte Nullstelle bei 1, einfache bei 0
B4: $ t^3-t^2 = t^2\cdot (t-1)$. Doppelte Nullstelle bei 1, einfache bei 0
Beim Auswechseln von $ t$ gegen $ (1-t)$ wird aus B4 $ (1-t)^2\cdot t$ , also B3 und aus B2 $ -t^2 \cdot (2t-3)$ wird $ (1-t)^2 \cdot (2t+1)$, also B1.

Lösung zum Selbsttest

 

T711 - Im Quadrarurproblem hängt die Ableitung nur von der unabhängigen Variablen x ab.
  -3 mal 2 = 6  - Man muss die Lösung ysol gegen tsol plotten nicht nur ysol allein.
  - Damit die Signatur (Struktur der Parameter beim Aufruf) für die im innern aufgerufene Ableitungfunktion immer gleich ist.

T712 $ dV=1.3^2\pi \cdot dh$ $ dV/dt = \sqrt{2 \cdot 9.81\cdot h} \cdot 0.04^2\pi$ $ dh/dt = \sqrt{2\cdot 9.81\cdot h} \cdot 0.04^2\pi /(1.3^2\pi) $ 

% deri = tankleerderi(tac,yac) Ableitung Tank-Entleerung
function deri = tankleerderi(tac,yac)
if yac > 0 % Absichern: Wurzelnenner muss positiv sein
  deri= -sqrt(2 * 9.81 * yac) * 0.04^2*pi/(1.3^2*pi);
else
  deri=0;
end

T713 

% varimagderi Ableitung Teilchen im variablen Magnetfeld
function deri = varimagderi(tac,yac)
B=0.1*yac(1);
deri = zeros(4,1); deri(1)=yac(2); deri(2) = 1/B*yac(4);
deri(3)=yac(4); deri(4) = -1/B*yac(2);

T714 

% circmotionderi  Ableitung zu Kreisbewegung
function deri = circmotionderi(tac,yac)
deri = zeros(4,1); deri(1)=yac(2); deri(2) = 0.05*yac(4);
deri(3)=yac(4); deri(4) = -0.05*yac(2);


  yvec0 dyvec0  yvec1 dyvec1    yvec2   dyvec2   yvec3 
 x   0   1       0.2    1       0.4     0.9999    0.6
 u   1   0       1     -0.0005  0.9999  -0.001    0.9997
 y  20   0       20    -0.01   19.998   -0.02   19.994
 v   0 -0.05    -0.01  -0.05   -0.02    -0.05    -0.03
 t = 0           0.2            0.4             0.6

T715 

% deri= fallluftderi(tac,yac) Ableitung
%  freier Fall mit Luftwiderstand
function deri = fallluftderi(tac,yac)
deri = zeros(2,1); deri(1)=yac(2);
% a) deri(2) = -9.81
deri(2) = -9.81 + deri(2)^2*0.05;


Unterabschnitte
next up previous contents
Nächste Seite: Lösungshinweise zum Kapitel 8 Aufwärts: Lösungshinweise Vorherige Seite: Lösungshinweise zum Kapitel 6   Inhalt
Stefan Adam 2006-03-07