



Nächste Seite: Lissajous-Figuren
Aufwärts: Übungen zum Kapitel 2
Vorherige Seite: Übungen zum Kapitel 2
Inhalt
Unterabschnitte
Schreiben Sie ein Skript-M-File, das eine gerade (bzw. ungerade)
Funktion grafisch darstellt. Programmieren Sie darin mit
v=input('Testwert-Eingabe') die Abfrage eines x-Wertes.
Zeichnen Sie aufgrund dieses x-Wertes die Verbindungslinie
zwischen den Punkten (-x/y) (0/y) (x/y) für die gerade Funktion,
bzw. (-x/-y) (0/0) (x/y) für die ungerade Funktion.
Eine Lösung dieser Aufgabe ist in den Beispiel-M-Files im Anhang enthalten.
Schreiben Sie ein Skript-M-File, das eine periodische
Funktion über mehrere Perioden der Länge 'T' grafisch darstellt.
Programmieren Sie darin mit
v=input('Testwert-Eingabe') die Abfrage eines x-Wertes.
Basierend auf diesem x-Wert demonstriert die Verbindungslinie
zwischen den Punkten ( x / y ) und ( (x+T) /
y ) grafisch die
Periodizitätsbedingung.
Eine Lösung dieser Aufgabe ist in den Beispiel-M-Files im Anhang enthalten.
Stellen Sie die Sinus- und Kosinusfunktionen mit verschiedenen Farben in einem
gemeinsamen Plot dar.
Erstellen Sie ein M-File Skript, das die Sinus- und Kosinusfunktionen in einem
gemeinsamen Plot mit verschiedenen Farben darstellt. Anschließend
sollen durch zwei interaktive Abfragen der Art
a = input('cos-Faktor?') die Gewichte a und b
bestimmt werden und in einer dritten Farbe
f3(w) = a*cos(w) + b*sin(w) dazu gezeichnet werden.
Mit dem untenstehenden, speziellen M-File, einem sogenannten Funktions-M-File
kann man die zu zeichnende Funktion als String (Zeichenkettenparameter)
in Klammern eingeben z.B. genfcplot('sin').
function y = genfcplot(fctnam)
x = 0.01:0.01:5 ;
y = feval(fctnam, x) ;
plot(x,y) ;
Zeichnen Sie die Funktionskurve der ,,Versiera di Agnesi``:
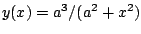 für
für 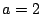 .
.
Mit verschiedenen Exponenten 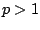 erhält man aus der Formel
erhält man aus der Formel
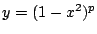 mit
mit
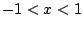 verschiedene Glockenkurven.
Stellen Sie diese in einer gemeinsamen Grafik dar!
verschiedene Glockenkurven.
Stellen Sie diese in einer gemeinsamen Grafik dar!




Nächste Seite: Lissajous-Figuren
Aufwärts: Übungen zum Kapitel 2
Vorherige Seite: Übungen zum Kapitel 2
Inhalt
Stefan Adam
2006-03-07