



Nächste Seite: Selbsttests zum Kapitel 2
Aufwärts: Elementarmathematik aktivieren
Vorherige Seite: Grafiken mit komplexen Zahlen
Inhalt
Miniprojekte zur Elementarmathematik
Beim ersten rechtwinkligen Dreieck haben beiden Katheten die Länge 1.
Platzieren Sie dieses im Koordinatensystem so, dass die Ecken bei (0/0),
(1/0) und (1/1) liegen. Die Hypotenuse hat dann die Länge 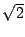 und zeigt in die 45
und zeigt in die 45
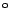 -Richtung. Für jedes nachfolgende Dreieck wird
die Hypotenuse des vorangegangenen zur neuen Kathete und am äußeren Punkt
wird eine Kathete der Länge 1 angefügt
(im rechten Winkel, versteht sich).
-Richtung. Für jedes nachfolgende Dreieck wird
die Hypotenuse des vorangegangenen zur neuen Kathete und am äußeren Punkt
wird eine Kathete der Länge 1 angefügt
(im rechten Winkel, versteht sich).
Nach dem Satz von Pythagoras erhalten die Katheten die Längen
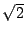 ,
, 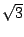 ,
,
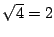 ,
, 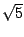 ,
, 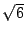 , etc. und
die Winkel beim Nullpunkt werden immer kleiner. Erstellen Sie ein
MATLAB M-File, das eine solche Serie von Dreiecken zeichnet und
probieren Sie aus, wieviele Dreiecke man braucht, um bis zu 360
, etc. und
die Winkel beim Nullpunkt werden immer kleiner. Erstellen Sie ein
MATLAB M-File, das eine solche Serie von Dreiecken zeichnet und
probieren Sie aus, wieviele Dreiecke man braucht, um bis zu 360
 zu kommen. Freuen Sie sich an der hübschen Figur!
zu kommen. Freuen Sie sich an der hübschen Figur!
Benutzen Sie 3D Kurven in Parameterdarstellung zum Visualisieren
eines Moebius-Bandes. Dazu muss eine kurze Strecke, deren Mittelpunkt auf
einem Kreis verläuft und die immer in einer radialen Ebene bleibt,
zusätzlich eine halbe Drehung (180
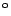 ) um eine
tangentiale Achse pro Umlauf um den Kreis ausführen.
) um eine
tangentiale Achse pro Umlauf um den Kreis ausführen.
Erzeugen Sie ein M-File, das einen Film nach dem folgenden Drehbuch
ablaufen lässt:
In der ersten Phase wird aus dem Punkt (0/1) heraus ein gleichseitiges
Dreieck generiert, das bereits beim Aufbau immer im Einheitskreis
einbeschrieben ist. Jede Seite bildet zuerst eine immer länger
werdende Sehne, solange bis sie die Seitenlänge des gleichseitigen Dreiecks
erreicht hat. Dann bildet sich eine Ecke und die nächste Sehne startet
mit der Länge 0 und wird immer länger, während
die vorher produzierte Seite (bzw. Seiten) sich weiter dreht (drehen).
Dies geht so lange, bis alle drei Sehnen, eine nach der anderen, die richtige
Länge erreicht haben; dann ist das gleichseitige Dreieck fertig.
In den folgenden Phasen wird das Dreieck zum Quadrat ergänzt, dann
das Quadrat zum regulären 5-Eck und so weiter bis ca. zum Achteck.
Jedesmal beim Erweitern werden die bisherigen Seiten kürzer und drehen sich,
um der langsam zur Länge der neuen Seite
anwachsenden Sehne Platz zu machen.
Das Rückwärtslaufen dieses Films ist ebenso spannend, wenn der
Punkt (0/1) die Linie langsam wieder auffrisst.
Erstellen Sie einen Film, welcher, ausgehend von der
Wellengleichung
die Abfolge der Funktionen
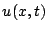 in Abhängigkeit von
in Abhängigkeit von 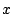 für die verschiedenen Werte von
für die verschiedenen Werte von 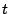 ,
,
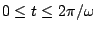 , aufeinander folgend zeigt.
, aufeinander folgend zeigt.
Wählen Sie also einen Wert für 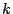 , dazugehörig einen Plot-Bereich, so
dass
, dazugehörig einen Plot-Bereich, so
dass
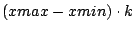 mindestens 4, eher aber 7-8 ganze Wellenformen
ergibt. Dann brauchen Sie nur noch etwa 20 bis 30 Varianten dieser
Wellen für verschiedene Zeitpunkte nacheinander zu zeichnen und
jeweils die
vorhergehende Wellenform zu löschen.
mindestens 4, eher aber 7-8 ganze Wellenformen
ergibt. Dann brauchen Sie nur noch etwa 20 bis 30 Varianten dieser
Wellen für verschiedene Zeitpunkte nacheinander zu zeichnen und
jeweils die
vorhergehende Wellenform zu löschen.
Unterabschnitte




Nächste Seite: Selbsttests zum Kapitel 2
Aufwärts: Elementarmathematik aktivieren
Vorherige Seite: Grafiken mit komplexen Zahlen
Inhalt
Stefan Adam
2006-03-07