



Nächste Seite: Miniprojekte zur Elementarmathematik
Aufwärts: Übungen zum Kapitel 2
Vorherige Seite: Komplexe Zahlen
Inhalt
Unterabschnitte
Erstellen Sie ein M-File, bei dem mit der Funktion
val=input('Prompt-Text') die Anzahl Ecken abgefragt wird, und
das anschließend das entsprechende reguläre Polygon zeichnet.
Erzeugen Sie eine Grafik
des Einheitskreises in der Gauß'schen Zahlenebene
mit der komplexen Exponentialfunktion:
-
- w = 2*pi*(0:0.01:1); c = exp(j*w); plot(c)
Modifizieren Sie den komplexen Einheitskreis
(w = 2*pi*(0:0.01:1); c = exp(j*w)) zu verschiedenen
Ellipsen mit verschiedenen reellen und komplexen Werten von A und B:
-
- e = A*real(c) + B*j*imag(c) ; plot(e)
Lösen Sie die Übung 20-18 (Kepler-Ellipse), in der kartesischen
Darstellung
mit verschiedenen Werten von
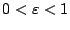 und vergleichen Sie
diese mit den Ellipsen der Übung 20-29.
Entdecken Sie den wichtigsten Unterschied zwischen den beiden
grafischen Darstellungen der Ellipse!
und vergleichen Sie
diese mit den Ellipsen der Übung 20-29.
Entdecken Sie den wichtigsten Unterschied zwischen den beiden
grafischen Darstellungen der Ellipse!
Mit t = w/2/pi; p = f*t + c; plot(p) erhalten Sie je nach den Werten des Gewichtsfaktors f
verschiedene Pseudozykloiden. (c ist dabei der komplex definierte
Einheitskreis mit mehreren Umgängen (w = 2*pi*(0:0.01:6); c = exp(j*w))
Experimentieren Sie mit den Grenzwinkelwerten w1 und w2, sowie
mit dem Vorschubfaktor k, bis die Figur
-
- w = w1:0.01:w2; z = exp(j*w)-k*w; plot(z)
die Form einer Brezel ergibt.
Erzeugen Sie eine Grafik, in der eine Spirale durch die
aufeinander folgenden Werte von aufsteigenden Potenzen
einer komplexen Zahl definiert wird, also durch 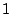 ,
, 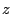 ,
, 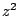 ,
, 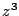 etc.
(z.B.
etc.
(z.B.
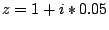 ).
).
Überlegen Sie sich, wie man zwischen den Punkten interpolieren könnte,
da diese Spirale für gewisse Zahlen etwas eckig wird!




Nächste Seite: Miniprojekte zur Elementarmathematik
Aufwärts: Übungen zum Kapitel 2
Vorherige Seite: Komplexe Zahlen
Inhalt
Stefan Adam
2006-03-07