



Nächste Seite: Grafiken mit komplexen Zahlen
Aufwärts: Übungen zum Kapitel 2
Vorherige Seite: Folgen und Reihen
Inhalt
Unterabschnitte
Programmieren Sie die grafische Darstellung
der Addition von zwei komplexen Zahlen in der Gauß'schen Zahlenebene!
(Funktions-M-file mit zwei komplexen Zahlen als Eingabe und der Summe als
Rückgabewert, sowie der gemeinsamen
grafischen Darstellung der drei Zahlen (Vektoren),
je in verschiedenen Farben).
Durch Bilden der Summe und der Differenz der Euler'sche Identität
für positive und negative Winkel:
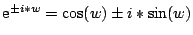 erhält man die
bekannten Formeln,
welche die Funktionen cos(w) und sin(w) durch
Exponentialfunktionen von w (bzw. von i*w) auszudrücken.
Führen Sie diese Berechnungen selbst aus und
kontrollieren Sie Ihr Resultat mit der Formelsammlung!
erhält man die
bekannten Formeln,
welche die Funktionen cos(w) und sin(w) durch
Exponentialfunktionen von w (bzw. von i*w) auszudrücken.
Führen Sie diese Berechnungen selbst aus und
kontrollieren Sie Ihr Resultat mit der Formelsammlung!
Wenn man die Euler'sche Identität potenziert, so
erhält man die Moivre'schen Formeln:
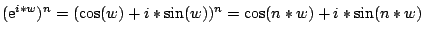 ,
Benutzen Sie diese sowie die binomischen Formeln, um
die bekannten Formeln für
die trigonometrischen Funktionen für doppelte und dreifache Winkel
selbst herzuleiten.
,
Benutzen Sie diese sowie die binomischen Formeln, um
die bekannten Formeln für
die trigonometrischen Funktionen für doppelte und dreifache Winkel
selbst herzuleiten.
Suchen Sie alle Lösungen der Gleichung
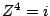 . Beachten Sie die kleinen aber wesentlichen
Unterschiede zu den Lösungen des wohlbekannten Problems
. Beachten Sie die kleinen aber wesentlichen
Unterschiede zu den Lösungen des wohlbekannten Problems 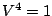 .
.




Nächste Seite: Grafiken mit komplexen Zahlen
Aufwärts: Übungen zum Kapitel 2
Vorherige Seite: Folgen und Reihen
Inhalt
Stefan Adam
2006-03-07