Testserie 3.2

T321

Verständnisfragen

-

Wie erhält man zu einem gegebenen Gleichungssystem das zugehörige homogene Gleichungssystem?

-

Beschreiben Sie Bildraum und Nullraum für die Matrix
A= [ 1 0 1 ; 0 0 0 ; 0 1 -1].

-

Welches ist der Rang einer Turmmatrix und welches derjenige einer Spechtmatrix?

-

Wie nennt man eine Matrix für welche gilt: $A^T = A^{-1}$?

T322

Schleifenprogrammierung
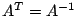Erstellen Sie ein Skript-M-File, welches für beliebig vorgegebenes 'n' eine Matrix erzeugt mit den Werten 2 auf der Diagonalen und den Werten '-1' auf den beiden Parallelen zur Diagonalen im Abstand 2. Auf den Nebendiagonalen und außerhalb der '-1'-Linie sind die Werte Null.

T323

Test auf Antisymmetrie
Schreiben Sie ein Funktions-M-File, welches eine Matrix als Eingabe verwendet und 1 zurückgibt, falls diese Matrix antisymmetrisch ist, und Null im anderen Fall.

T324

Projektionsmatrizen
Geben Sie die drei Projektionsmatrizen an, welche die Vektoren des dreidimensionalen Raumes auf die x-Achse, die y-Achse und die z-Achse projizieren! Welchen Rang haben diese Matrizen?

T325

Betrag eines n-dimensionalen Vektors
Schreiben Sie ein Funktions-M-File, welches einen n-dimensionalen Vektor als Eingabe verwendet und daraus dessen Betrag bestimmt. (Ohne Verwendung der Bibliotheksfunktion norm(v). Die Funktionen length(v), size(v), sqrt(s) sind hingegen ausdrücklich erlaubt.)