



Nächste Seite: Vektorgeometrie in der Ebene
Aufwärts: Übungen zum Kapitel 4
Vorherige Seite: Übungen zum Kapitel 4
Inhalt
Unterabschnitte
Von einem Dreispitz (dreiseitige Pyramide) mit den Bodenpunkten
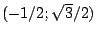 ,
,
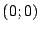 und
und
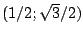 wird die Höhe gesucht, so dass der Winkel im Raum zwischen
je zwei der drei Kanten 90
wird die Höhe gesucht, so dass der Winkel im Raum zwischen
je zwei der drei Kanten 90
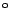 ist.
Wie groß ist dann die wahre Kantenlänge?
ist.
Wie groß ist dann die wahre Kantenlänge?
Ein Turm mit der Dachform einer vierseitigen Pyramide hat einen
quadratischen Grundriss von 12 Meter Seitenlänge. Die
Spitze des Turmes liegt 10 Meter über der unteren Dachkante.
Wie groß ist der Neigungswinkel der Dachflächen (gegenüber der
Horizontalen)? Berechnen Sie auch den wahren Winkel zwischen
zwei aneinander angrenzenden Dachflächen.
Berechnen Sie die Winkel zwischen der Körperdiagonalen,
welche die Punkte (0/0/0) und (1/1/1) im 3D-Einheitswürfel
verbindet, und den 6 verschiedenen Richtungen von Flächendiagonalen!
Stefan Adam
2006-03-07