Vektorgeometrie in der Ebene

40-4  Hesse'sche Normalform in der Ebene

 
Stellvertretend für die Gleichung einer Ebene im Raum soll die Gerade in der Ebene, welche durch die Punkte A=(4 /0) und B=(0/3) geht, in der Hesse'schen Normalform dargestellt werden. Dies erreicht man in folgenden Schritten:

-

der senkrecht auf der Geraden stehende Vektor (Normalenvektor) ist zu bestimmen. Empfohlenes Vorzeichen: positiv im I. Quadranten.

-

Normierung zu Einheitsvektor $e_n$

-

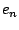
Ansatz der Geradengleichung in der Hesse'schen Normalform:
$e_n \cdot OP - e_n \cdot OA = 0$.

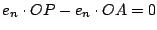Testen Sie Punkte A und B und einen weiteren selbstgewählten Punkt auf Ihre Abstandswerte zu dieser Geraden.

40-5  Visualisierung der Hesse'schen Normalform

 
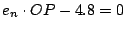Erstellen Sie ein MATLAB-Skript, an das Sie mit dem Befehl x = input('x-Wert') bzw. y = input('y-Wert') zwei Koordinaten übergeben. Diese sollen anschließend als Originalvektor OP in der Ebene eingezeichnet werden. Ferner sollen die Projektion von OP auf $e_n = [ 0.8~ 0.6]'$ sowie die Gerade $e_n \cdot OP - 4.8 = 0$ (geht durch A= (6/0) und B=(0/8) eingezeichnet werden.
Als Zahlenausgabe sollen Sie den Ausdruck 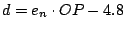$d = e_n \cdot OP - 4.8$ auswerten, der genau dann Null wird, falls der eingegebene Punkt auf der Geraden liegt. (Dann liegt auch der Endpunkt des projizierten Vektors auf der Geraden.)
Probieren Sie mit den eingegebenen Punkten die Gerade zu treffen.
Aussage der Hesse'schen Normalform: Eine Gerade (Ebene) umfasst alle Punkte, deren Ortsvektoren bei Projektion auf den Normaleneinheitsvektor dieselbe Länge 'd' ergeben.