



Nächste Seite: Ausflug in höhere Dimensionen
Aufwärts: Übungen zum Kapitel 4
Vorherige Seite: Vektorgeometrie in der Ebene
Inhalt
Unterabschnitte
Bestimmen Sie die vier Einheitsnormalenvektoren zu den Flächen eines
regulären Tetraeders, welcher mit der
Grundfläche auf der x-y-Ebene steht und eine Kante
parallel zur x-Achse hat.
Ein Oktaeder hat die Ecken A=(4/0/0), B=(0/4/0) ,
C=(-4/0/0), D=(0/-4/0), E=(0/0/4), F=(0/0/-4).
Zeichnen Sie diesen Oktaeder mit plot3() in 3D, indem
Sie die Punkte zu einem Linienzug zusammenstellen (einzelne Kanten
werden mehrfach durchlaufen).
Bestimmen Sie die Gerade (Geradengleichung in Punkt-Richtungs-Form),
welche den Mittelpunkt der Strecke DE mit dem Schwerpunkt des
Dreiecks ABE verbindet und suchen Sie den Durchstoßpunkt
dieser Geraden durch die x-y-Ebene! Zeichnen Sie diese Gerade mit den drei
speziellen Punkten in dieselbe Grafik ein!
Eine Pyramide mit gleichseitigen Dreiecken als Seitenflächen
mit der Kantenlänge 10 m hat ihre 4 Ecken genau
nach Norden, Osten, Süden
und Westen orientiert.
An einem Sommertag steht die Sonne 15
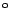 über dem Horizont, wenn sie
genau im Westen steht. Wie weit ist der Schatten der Pyramidenspitze
vom Zentrum der Grundfläche entfernt, und welchen Winkel
bilden dann die Schattengrenzen?
über dem Horizont, wenn sie
genau im Westen steht. Wie weit ist der Schatten der Pyramidenspitze
vom Zentrum der Grundfläche entfernt, und welchen Winkel
bilden dann die Schattengrenzen?
Suchen Sie die x-Koordinate des Punktes D=(x/0/0) so, dass
er mit den drei Punkten A=(0/0/4), B=(-4/3/3) und C=(0/4/0) in
derselben Ebene liegt. Berechnen sie anschließend den Schwerpunkt des
so entstandenen ebenen Vierecks (als gewichtetes Mittel aus zwei
Dreiecksschwerpunkten mit den Dreiecksflächen als Gewichte).
Bestimmen Sie die Hesse'sche Normalform der Ebene durch die Punkte
A=(3/0/0) , B=(0/4/0), C=(0/0/3.2) und berechnen sie den
Abstand des Koordinatenursprungs von dieser Ebene!




Nächste Seite: Ausflug in höhere Dimensionen
Aufwärts: Übungen zum Kapitel 4
Vorherige Seite: Vektorgeometrie in der Ebene
Inhalt
Stefan Adam
2006-03-07