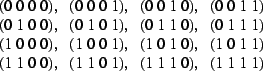Ausflug in höhere Dimensionen

40-11  Winkel im vierdimensionalen Raum:

 
Berechnen Sie die Winkel zwischen den vierdimensionalen Vektoren

Schreiben Sie ein M-File zur Winkelberechnung.

40-12  Winkel zwischen mehrdimensionalen Vektoren:

 
Berechnen Sie die Winkel zwischen allen Kombinationen der Vektoren $k,~f,~r,~v$

40-13   Zwei, drei und vierdimensionaler Einheits-,,Würfel``

 

-

Ein ,,Würfel`` in 2D hat die Ecken:

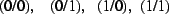
Daraus ergeben sich die Kantenvektoren [0 1]' und [1 0]', je 2-fach. (Alle möglichen Differenzen zwischen je 2 Ecken.)
Bestimmen Sie die Diagonalenvektoren!

-

Der echte Würfel in 3D hat die Ecken:

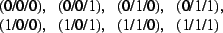
Bestimmen Sie die Kantenvektoren und deren Vielfachheit.
Suchen Sie die 2 verschiedenen Typen von Diagonalenvektoren! Bestimmen Sie deren Länge, sowie deren Winkel (je 3 Richtungskosinuswerte bezüglich der Koordinatenachsen).

-

Ein ,,Würfel`` in 4D, also 4D-Hypercube hat die Ecken:

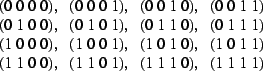
Suchen Sie auch für diesen Fall die Kantenvektoren mit deren Vielfachheit, sowie die (hier drei Typen von) Diagonalenvektoren mit deren Länge und deren (je 4) Winkeln!