



Nächste Seite: Homogene Koordinatentransformationen im Raum
Aufwärts: Übungen zum Kapitel 4
Vorherige Seite: Durch Matrizen definierte Abbildungen
Inhalt
Unterabschnitte
Das bereits bekannte ,,L``, definiert durch die
drei Punkte (5/2), (5/0) und (6/0),
soll in homogene Koordinaten umgeschrieben
werden, und
die Ortsvektoren der Dimension 3x1 zu einer 3x3 Punktematrix
zusammengestellt werden.
Gesucht sind die speziellen 3x3 Matrizen der homogenen Koordinaten,
die Bildkoordinaten und ebenfalls ein gemeinsamer Plot
von Bild und Urbild für die folgenden Abbildungen:
- a)
- Verschiebung der L-Ecke nach a
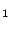 )(0/5), a
)(0/5), a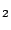 )(0/0) ,
a
)(0/0) ,
a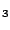 ) (-5/0)
) (-5/0)
- b)
- Drehung um 90 Grad um Ursprung
- c)
- Drehung um 45, sowie 90 Grad um die eigene Ecke des ,,L``
Das Übungs- ,,L`` (5/2) (5/0) (6/0) soll 3 mal um je 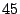
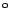 um den Koordinatenursprung gedreht werden.
um den Koordinatenursprung gedreht werden.
An den neuen Koordinaten sollen die gedrehten ,,L`` 's
um ihre Ecke um 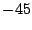
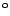 ,
,
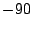
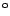 ,
, 
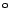 gedreht werden, so dass alle am neuen Ort
wieder aufrecht stehen.
gedreht werden, so dass alle am neuen Ort
wieder aufrecht stehen.
Wenn Sie die ursprüngliche Drehung, und dann von links die Drehung
um die Ecke in homogenen Koordinaten zusammenmultiplizieren, so werden
nur noch Translationen übrigbleiben.
Schreiben Sie ein Skript zur Erzeugung und anschließenden Anwendung
der Transformationsmatrix in homogenen Koordinaten, welche den
Eckpunkt des ,,L`` um einen vorgegebenen Winkel um den Ursprung
dreht und gleichzeitig die ,,L``-Figur in entgegengesetzter
Richtung um ihre Ecke um denselben Winkel dreht.
Die Ecke des ,,L``, definiert durch die
drei Punkte (5/2), (5/0) und (6/0)
soll um den allgemeinen Winkelparameter 'w' auf einem Kreis
(mit dem Radius 5) bewegt werden. Dabei soll
- a)
- Die Orientierung des ,,L`` (vertikal) bei der Bewegung erhalten bleiben.
- b)
- Das ,,L`` eine Drehung
um den Winkel -w (Gegendrehung mit gleichem Winkelbetrag) ausführen.
Bestimmen Sie für die beiden Fälle die homogenen
Transformationsmatrizen, je als Funktion des Winkels 'w' und testen Sie
diese Abbildungen mit einem Plot des abgebildeten ,,L``!
Gegeben Sei ein gleichseitiges Dreieck A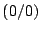 , B
, B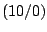 ,
C
,
C
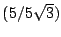 .
.
Gesucht sind die zwei Transformationsmatrizen in homogenen Koordinaten,
welche das Dreieck auf sich selbst abbilden und zwar
- a)
- A' = B, B' = C, C' = A
und
- b)
- A'' = C, B'' = A, C'' = B.
Zeigen Sie dass
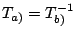 ist!
ist!
Das Rechteck 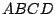 ,
, 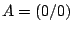 ,
, 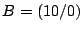 ,
, 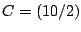 ,
, 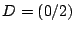 soll um den Punkt
soll um den Punkt 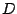 um
um
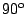 gedreht werden. Das einmal gedrehte
Rechteck
gedreht werden. Das einmal gedrehte
Rechteck
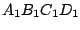 soll anschliessend um den Punkt
soll anschliessend um den Punkt 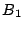 ebenfalls um
ebenfalls um
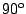 gedreht werden, dann
gedreht werden, dann
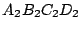 um
um
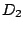 . So bilden die vier Rechtecke ein Quadrat
mit Seitenlänge 12 um einem Innenhof mit Seitenlänge 8. Führen Sie
diese Abbildungen in homogenen Koordinaten aus und stellen sie grafisch dar.
Zeigen Sie, dass,
zusammen mit einer vierten Rotation um
. So bilden die vier Rechtecke ein Quadrat
mit Seitenlänge 12 um einem Innenhof mit Seitenlänge 8. Führen Sie
diese Abbildungen in homogenen Koordinaten aus und stellen sie grafisch dar.
Zeigen Sie, dass,
zusammen mit einer vierten Rotation um 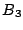 , die aus allen vier
Gesamttransformationen zusammengesetzte Transformationsmatrix die
Identität ergibt (
, die aus allen vier
Gesamttransformationen zusammengesetzte Transformationsmatrix die
Identität ergibt (
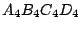 ist wieder
ist wieder 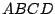 ).
).
Das Rechteck 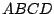 ,
, 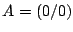 ,
, 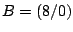 ,
, 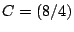 ,
, 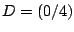 wird
einmal an der Geraden
wird
einmal an der Geraden 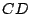 gespiegelt und als zweite Abbildung um den
Mittelpunkt der Strecke
gespiegelt und als zweite Abbildung um den
Mittelpunkt der Strecke 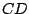 um 180
um 180
 gedreht.
Führen Sie diese beiden Transformationen in homogenen Koordinaten durch.
Zeigen Sie in einer Grafik, dass sich die beiden Bilder überdecken.
Die Überdeckung erfolge jedoch nicht Punkt für Punkt, deshalb gibt es
eine Korrespondenz-Tabelle der Art
gedreht.
Führen Sie diese beiden Transformationen in homogenen Koordinaten durch.
Zeigen Sie in einer Grafik, dass sich die beiden Bilder überdecken.
Die Überdeckung erfolge jedoch nicht Punkt für Punkt, deshalb gibt es
eine Korrespondenz-Tabelle der Art 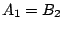 etc.
etc.




Nächste Seite: Homogene Koordinatentransformationen im Raum
Aufwärts: Übungen zum Kapitel 4
Vorherige Seite: Durch Matrizen definierte Abbildungen
Inhalt
Stefan Adam
2006-03-07