



Nächste Seite: Miniprojekte zur Raumgeometrie und
Aufwärts: Übungen zum Kapitel 4
Vorherige Seite: Homogene Koordinatentransformationen in der
Inhalt
Unterabschnitte
Das Dreibein mit den Ecken A=(0/0/0), B=(10/0/0), C(0/10/0) und
D=(0/0/10) soll einer Punktspiegelung am Punkt (5/5/5) unterworfen werden.
Der 3x3-Teil für die Punktspiegelung am Ursprung ist ( eye(3)).
eye(3)).
Für eine Wendeltreppe wird verinfachen angenommen,
sie sei aus quaderförmigegen Blöcken
der Dimension 100x50x18cm gebaut. Der Innenradius sei 50 cm. Jede
der 7 Stufen hat gegenüber der vorherigen eine Verdrehung von 15
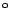 .
Bestimmen
Sie die Transformation in homogenen Koordinaten, die
von einem Block zum nächsten führt und erstellen
Sie eine 3D Figur der Treppe.
.
Bestimmen
Sie die Transformation in homogenen Koordinaten, die
von einem Block zum nächsten führt und erstellen
Sie eine 3D Figur der Treppe.
Ein Würfel mit den Ecken
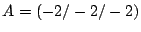 ,
,
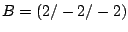 ,
,
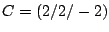 ,
,
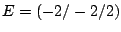 , etc. soll an seinen 8 Ecken je durch eine räumliche
Punktspiegelung nach aussen transformiert werden. Erstellen Sie eine
3D Grafik dieses Gebildes, das von den 27 Würfelplätzen im
dreifach erweiterten Volumen nur 9 Plätze ausfüllt!
, etc. soll an seinen 8 Ecken je durch eine räumliche
Punktspiegelung nach aussen transformiert werden. Erstellen Sie eine
3D Grafik dieses Gebildes, das von den 27 Würfelplätzen im
dreifach erweiterten Volumen nur 9 Plätze ausfüllt!
Ein 2 Meter grosses ``L'' mit 1 Meter Fusslänge steht aufrecht beim
Punkt [2 -4 0]' und dreht sich um die z-Achse.
Die x-z-Ebene sei ein Spiegel mit den Ecken (0/0/0) (4/0/0) (4/0/3)
(0/0/3). Zeichnen Sie die 3D-Parallelperspektive von ,,L``, seinem
Spiegelbild und den Spiegelrändern
von einem Punkt im Azimut im Bereich 290
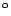 bis 310
bis 310
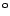 aus.
Der Betrachtungspunkt soll etwas oberhalb der x-y-Ebene liegen.
aus.
Der Betrachtungspunkt soll etwas oberhalb der x-y-Ebene liegen.
Die Eckpunkte eines Würfels mit Kantenlänge 2 ABCD-EFGH:
![\begin{sourcett}[-1 -1 -1]',[1 -1 -1]',[1 1 -1]',[-1 1 -1]',\\ {}
[-1 -1 1]',[1 -1 1]',[1 1 1]',[-1 1 1]'
\end{sourcett}](img315.png)
werden von jeder Fläche aus mit einer darüberliegenden Spitze TWNSOU
![\begin{sourcett}
(\texttt{[6 0 0]', [-6 0 0]', [0 6 0]', [0 -6 0]', [0 0 6]',[0 0 -6]'}
\end{sourcett}](img316.png)
zu einer Pyramide verbunden. Dies ergibt einen 3D-Stern mit 6 Spitzen.
Suchen Sie eine Punktfolge dieser 14 Punkte, so dass alle Kanten
durchlaufen werden. Erzeugen Sie die dazugehörige Vektorzusammenstellungsmatrix, um diesen Stern in einem Plot-Aufruf zu zeichnen.
Durch homogene Koordinatentransformationen im 3D soll dieser Stern
je in x- und y-Richtung um 15 cm verschoben kopiert werden.
Erzeugen Sie anschließend ein gedrehtes Bild dieser Anordnung
von 5 Sternen und ändern Sie die Betrachtungswinkel.
Die folgenden Befehle definieren in MATLAB die Eckpunkte und einen Linienzug,
der ein einfaches Haus zeichnet (in homogenen Koordinaten).
![\begin{sourcett}
v1 = [ 3 -2 0 1]' ;\\
v2 = [ 3 -2 3 1]' ;\\
v3 = [ 3 0 5 1]' ...
... ];\\ [0.2em]
lxi = H(1,:) ; ~~
lyi = H(2,:) ; ~~
lzi = H(3,:) ;
\end{sourcett}](img317.png)
Wenden Sie zuerst eine 3D-Rotation in homogenen Koordinaten
um die z-Achse um den (beliebigen) Winkel w
an. Anschließend
soll eine Rotation um den Winkel  t (negativ, weniger als 25 Grad)
um die neue y'-Achse erfolgen, um das Haus vom Helikopter aus zu sehen!
Achtung! Winkel von Grad in Radiant umrechnen.
t (negativ, weniger als 25 Grad)
um die neue y'-Achse erfolgen, um das Haus vom Helikopter aus zu sehen!
Achtung! Winkel von Grad in Radiant umrechnen.
Die Darstellung mit plot3(Hrot(1,:), Hrot(2,:), Hrot(2,:))
kann analog zum 2-dimensionalen
Fall mit axis ([ xmin, xmax, ymin, ymax, zmin, zmax]) und
axis square
ergänzt werden.




Nächste Seite: Miniprojekte zur Raumgeometrie und
Aufwärts: Übungen zum Kapitel 4
Vorherige Seite: Homogene Koordinatentransformationen in der
Inhalt
Stefan Adam
2006-03-07
![\begin{sourcett}
v1 = [ 3 -2 0 1]' ;\\
v2 = [ 3 -2 3 1]' ;\\
v3 = [ 3 0 5 1]' ...
... ];\\ [0.2em]
lxi = H(1,:) ; ~~
lyi = H(2,:) ; ~~
lzi = H(3,:) ;
\end{sourcett}](img317.png)