Miniprojekte zur Raumgeometrie und den Abbildungen

401   Generieren der fünf Platonischen Körper

 
Die fünf Platonischen Körper sind die einzigen Körper im dreidimensionalen Raum, welche von lauter gleichen regulären Polygonen begrenzt sind und bei welchen an jeder Ecke gleichviele Flächen aneinanderstoßen. Tetraeder, Oktaeder und Ikosaeder sind von gleichseitigen Dreiecken begrenzt, mit 3, 4 bzw. 5 Dreiecken die in jeder Ecke zusammenstoßen. Der Würfel, auch Hexaeder genannt, besteht aus Quadraten von denen je drei an jeder Ecke zusammenstoßen. Beim Dodekaeder (auch Pentagon-Dodekaeder) stoßen je drei Fünfecke in einer Ecke zusammen.

Durch eine Drehung um die y-Achse um den Winkel unter dem eine Kante vom Zentrum der umspannenden Kugel gesehen wird, ist eine Kante festlegbar zwischen dem Bild des höchsten Punktes auf der Kugel und dem aktuellen höchsten Punkt. Durch Drehen um die z-Achse um 1/3, 1/4 bzw. 1/5 Umdrehung können weitere Kanten festgelegt werden. Durch Hinzunehmen einer Drehung um 180 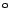$^{\mathrm{o}}$um die z-Achse können alle fünf Polyeder sukzessive durch Drehungen und Hinzufügen des jeweils obersten Punktes aufgebaut werden.

402   Suchen der Großkreis-Flugrouten

 
Zwischen zwei Orten auf der Erdkugel, deren Positionen in Längen- und Breitengrad-Angaben bekannt sind, soll der direkt verbindende Großkreis, die Distanz, sowie die Abflugrichtung und und die höchste auf diesem Großkreis erreichte Breite bestimmt werden.

403  Visualisieren eines Tetraeder-Rings beim Umstülpen

 
Sechs leicht verlängerte Tetraeder (mit einem gleichseitigen Dreieck als Mittelebenen-Schnitt, und gleichschenkligen Dreiecken mit einem etwas spitzeren Winkel zwischen den gleichen Schenkeln als Begrenzungsflächen) können zu einem Ring zusammenfügt werden. In der Grundstellung liegen drei der aneinanderstoßenden Kanten von Nachbar-Tetraedern in der Mittelebene, die drei anderen gemeinsamen Kanten stehen dann senkrecht zur Mittelebene. Wenn die Verbindungen zwischen je zwei Tetraedern um die momentane Achsenrichtung der gemeinsamen Kante drehbar sind, so läßt sich das ganze Gebilde umstülpen. Diese Bewegung kann in 3D grafisch dargestellt werden.

404   Die Bewegung eines Autos auf einer Parkhausrampe

 
Mit 3D homogenen Koordinatentransformationen läßt sich die Bewegung eines Autos modellieren, das eine wendelförmige Parkhausrampe hinauffährt.