



Nächste Seite: Partielle Ableitungen
Aufwärts: Übungen zum Kapitel 6
Vorherige Seite: Übungen zum Kapitel 6
Inhalt
Unterabschnitte
Orientieren Sie sich anhand der Hilfefunktion von MATLAB
über die Möglichkeiten zum Erstellen von Konturplots (contour).
Stellen Sie die Oberfläche einer
nach oben gewölbten Halbkugel grafisch dar.
Die Werte außerhalb des Äquators sollen Null gesetzt werden
(bzw. Null bleiben, wenn man mit zeros() beginnt).
Zeichnen Sie einen Konturplot der Funktion
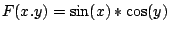 im Bereich
im Bereich
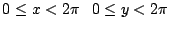 und suchen Sie
darin alle Punkte für die gleichzeitig gilt
und suchen Sie
darin alle Punkte für die gleichzeitig gilt
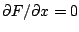 und
und
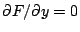
Füllen Sie eine rechteckige Matrix mit den Höhenwerten des Beispiels
mit dem Jurahügel:
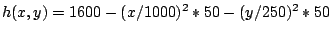 entsprechend den Intervallen
entsprechend den Intervallen
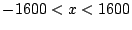 und
und
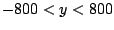 . Ein noch besseres Bild ergibt sich mit max(h,1200), das
entspricht dem Hügelteil über dem Nebelmeer.
. Ein noch besseres Bild ergibt sich mit max(h,1200), das
entspricht dem Hügelteil über dem Nebelmeer.
Stellen Sie diese Funktion mit 'contour' und 'surf' grafisch dar.
Verwenden Sie die Index-Anzeige-Matrix A aus den
Schleifen-Programmierübungen mit 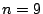 als Eingabefunktion für eine Kontur- oder Surf-Darstellung.
als Eingabefunktion für eine Kontur- oder Surf-Darstellung.
Ebenso eignen sich die oberen und unteren Dreiecksmatrizen mit
den Werten, welche mit dem Abstand von der Diagonalen ansteigen,
zur grafischen Darstellung als Fläche.
Mit der oberen Dreiecksmatrix Du dieses Typs erhalten Sie
durch Ph = [ Du fliplr(Du) ] und
P = [ flipud(Ph) ; Ph ] die Funktion einer Pyramide.
Vergleichen Sie die Kontur-/Surf-Formen der folgenden nxn Matrizen
miteinander (n ca. zwischen 9 und 20). ('Du' ist eine obere Diagonalmatrix
mit Werten, welche mit der Distanz zur Diagonalen zunehmen.)
-
- Du, Du*Du, Du.*Du, Du 3 , Du. 3
C=fliplr(Du), C*C, C.*C, C 3 , C. 3
Bestimmen Sie eine Funktion, welche die Form eines Trichters
beschreibt. Durchmesser der Ausflussöffnung 1 cm, Randdurchmesser
21 cm, Neigung 45
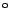 .
.
Entwerfen Sie eine Funktion, welche die Oberflächenform eines
gut gefüllten Kissens beschreibt!
Ein auf einem flachen Platz von 2x6 m aufgeschütteter
Haufen von Silofutter wird mit einer Plane zugedeckt und mit Seilen
festgebunden.
Die Höhe des Haufens über dem Platz sei durch die Funktion
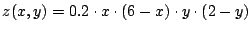 gegeben.
gegeben.
Berechnen Sie das Gesamtvolumen dieses Bodenspeichers.
Bestimmen Sie die 3D-Parameterdarstellung des Verlaufes von
einigen der Fixierseile, welche zwischen den 16 Pflöcken
(in den Ecken und 1 Pflock pro Meter) diagonal gespannt sind
(Richtung im Grundriss 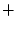 45
45
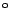 und
und  45
45
 ).
).
Stellen Sie zur Kontrolle die Fläche und die Seile mit
MATLAB 3D-Grafik dar.
Ausblick: Bestimmen Sie das Restvolumen als Funktion der
x-Position, bis zu welcher der Haufen bereits abgetragen ist.




Nächste Seite: Partielle Ableitungen
Aufwärts: Übungen zum Kapitel 6
Vorherige Seite: Übungen zum Kapitel 6
Inhalt
Stefan Adam
2006-03-07