



Nächste Seite: Fitprobleme
Aufwärts: Übungen zum Kapitel 6
Vorherige Seite: Funktionsdarstellung
Inhalt
Unterabschnitte
Bestimmen Sie je alle möglichen partiellen Ableitungen
der folgenden Funktionen:
- a)
-
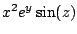
- b)
-
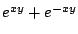
- c)
-
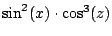
- d)
-
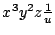
Bestimmen Sie jeweils analytisch alle partiellen Ableitungen
der untenstehenden Funktionen:
a)
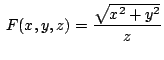
b)
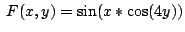
c)
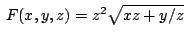
Bestimmen Sie je
![$ \mathrm{grad} F = \displaystyle\left[ \frac{ \partial{ F}}{ \partial{ x}}
~~\frac{\partial{F}}{\partial y} ~~\frac{\partial{F}}{\partial z} \right]'$](img371.png)
- a)
-
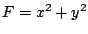
- b)
-
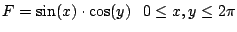
- c)
-
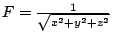
Zeichnen Sie die zuerst die Höhenlinien der Funktion
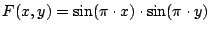 im Bereich
im Bereich
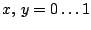
Darin soll nun ein Feld von kleinen Strichen (bzw Pfeilen)
eingezeichnet werden, welche die Gradientenvektoren darstellen.
Dazu existieren die Bibliotheksfunktionen gradient() quiver();
Bilden Sie die beiden partiellen Ableitungen der Jurahügelfunktion
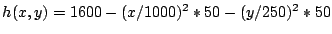 und stellen Sie diese ebenfalls je als zweidimensionale Funktion
dar!
und stellen Sie diese ebenfalls je als zweidimensionale Funktion
dar!
Zeichnen Sie in den Konturplot der Originalfunktion
die Gradientenvektoren
ein!
Zeichnen Sie die Höhenlinien und 3D-Flächendarstellungen (surf)
für die folgenden Funktionen: (alle im Bereich
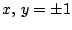 )
)
- a)
-
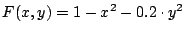
- b)
-
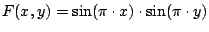
- c)
-
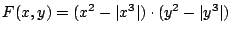
Der Gradientenvektor, d.h. die Einreihung der partiellen Ableitungen
als Komponenten eines Vektors, liefert eine Art Funktion von mehreren
Variablen mit der speziellen Eigenschaft, dass für jeden Punkt (bzw.
jede Kombination der unabhängigen Variablen) mehrere Funktionswerte
geliefert werden. Man nennt dies eine vektorwertige Funktion.
Bestimmen Sie die Gradientenvektoren der oben angegebenen Funktionen.
Suchen Sie die stationären Punkte (beide partiellen Ableitungen
gleichzeitig Null) in der Funktion
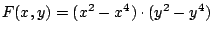 und vergleichen
Sie das Ergebnis mit den Formen der Höhenlinien in der
vorhergehenden Aufgabe!
und vergleichen
Sie das Ergebnis mit den Formen der Höhenlinien in der
vorhergehenden Aufgabe!
Zeichnen Sie einen Konturplot der biquartischen Funktion
(in beiden Richtungen vom 4. Grad),
welche im untenstehenden M-File
definiert wird. Berechnen Sie die partiellen
Ableitungen dieser Funktion und zeichnen Sie
Gradientenvektoren
in den Kontur-Plot ein!
for k=1:50
for l = 1:50
x = (k -26)*0.07; y = (l-26)*0.07;
V(l,k)=(0.25*x^4-0.5*x^2)-0.12*x +(0.25*y^4-0.5*y^2)+1-0.05*y;
end
end
Das elektrische Potential einer Punktladung ist
gegeben durch die Formel:
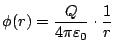 Dabei ist Q die Ladung und
Dabei ist Q die Ladung und
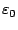 die Dielektrizitätskonstante.
Schreiben Sie diese Funktion in eine Funktion der kartesischen Koordinaten
die Dielektrizitätskonstante.
Schreiben Sie diese Funktion in eine Funktion der kartesischen Koordinaten 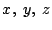 um und berechnen Sie die drei partiellen Ableitungen
analytisch, je ebenfalls als Funktionen der drei Variablen
um und berechnen Sie die drei partiellen Ableitungen
analytisch, je ebenfalls als Funktionen der drei Variablen 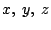 .
Durch Zusammenstellen dieser drei Funktionen als Gradientenvektor
erhalten Sie die
Vektorfunktion des elektrischen Feldes
.
Durch Zusammenstellen dieser drei Funktionen als Gradientenvektor
erhalten Sie die
Vektorfunktion des elektrischen Feldes
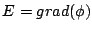 .
.




Nächste Seite: Fitprobleme
Aufwärts: Übungen zum Kapitel 6
Vorherige Seite: Funktionsdarstellung
Inhalt
Stefan Adam
2006-03-07
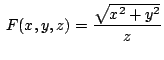
![$ \mathrm{grad} F = \displaystyle\left[ \frac{ \partial{ F}}{ \partial{ x}}
~~\frac{\partial{F}}{\partial y} ~~\frac{\partial{F}}{\partial z} \right]'$](img371.png)
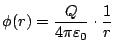 Dabei ist Q die Ladung und
Dabei ist Q die Ladung und