



Nächste Seite: Methode der Lagrange-Multiplikatoren
Aufwärts: Übungen zum Kapitel 6
Vorherige Seite: Partielle Ableitungen
Inhalt
Unterabschnitte
Bestimmen Sie die Gleichungen für einen Parabelfit
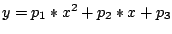 und einen Fit an eine
Funktion dritten Grades
und einen Fit an eine
Funktion dritten Grades
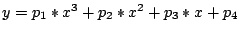 analog zur Herleitung für den Geradenfit.
analog zur Herleitung für den Geradenfit.
Dazu werden die partiellen Ableitungen der Zielfunktionen
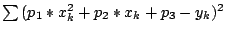 nach
nach
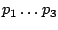 bzw.
bzw.
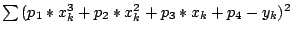 nach
nach
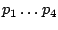 Null gesetzt werden.
Null gesetzt werden.
Programmieren Sie diese zwei Fälle sowie den Geradenfit
in MATLAB und wenden Sie die
M-Files auf die untenstehenden Punkte an!
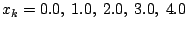
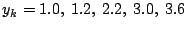
Suchen Sie die beste Kurve 3. Grades (bzw. die Koeffizienten
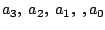 ) durch die Punkte
) durch die Punkte
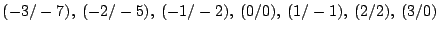 durch Aufstellen der Fehlergleichungen und anschließende Standard
MATLAB-Lösung.
durch Aufstellen der Fehlergleichungen und anschließende Standard
MATLAB-Lösung.
Bestimmen Sie nach dem Gauß'schen Ausgleichsprinzip die beste Gerade
durch die Punkte
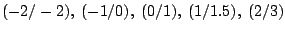
a) durch Lösen der Normalengleichungen
b) durch Aufstellen der Fehlergleichungen und MATLAB-Lösung
A
 b
b
Diese beiden Fits sollen anschließend wiederholt werden
unter Anwendung der Gewichte (4, 2, 1, 2, 4) für die gegebenen Punkte.
Vergleichen Sie die verschiedenen Resultate!
Wenn man die Formeln genauer analysiert, sieht man, dass
die einfachen Fitverfahren ein Problem der
Art
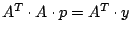 lösen.
lösen.
A ist dabei die Matrix aus den Vektoren
[ x. ^2 x ones(n,1) ]
In MATLAB kann man aber direkt das überbestimmte
Fehlergleichungssystem
lösen:
MATLAB löst mit
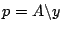 ein überbestimmtes System
ein überbestimmtes System
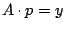 automatisch
im Sinne eines Fits!
automatisch
im Sinne eines Fits!
Lösen Sie die obigen Fitprobleme auch noch mit dem
viel einfacheren Prinzip der Fehlergleichungen!
Gegeben sind die Punkte (1/1) (2/3) (3/4) (4/2) (5/1).
Suchen Sie die bestem Parameter A, B, C, (evtl. D),
damit die Funktionen
- a)
-
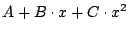
- b)
-
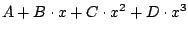
möglichst nahe an die Punkte kommen. Stellen Sie die
Funktionskurve und die Punkte mit MATLAB grafisch dar!
Lösen Sie jede der Aufgaben sowohl mit den Normalengleichungen
als auch mit den Fehlergleichungen und testen Sie jeweils
die Formel
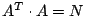 .
.
Schreiben Sie ein Skript-M-File, das einen Fit n
gegebenen Punkten  an eine Linearkombination von drei frei
festlegbaren Funktionen A*fitfun1(x)+ B*fitfun2(x) =C*fitfun3(x)
durchführt!
an eine Linearkombination von drei frei
festlegbaren Funktionen A*fitfun1(x)+ B*fitfun2(x) =C*fitfun3(x)
durchführt!
Testen Sie dieses, indem Sie 5 Punkte der Sinusfunktion
zwischen 0 und  wählen und als fitfun1 bis 3 die Konstante 1,
die Funktion
wählen und als fitfun1 bis 3 die Konstante 1,
die Funktion 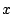 und die Funktion
und die Funktion 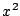 wählen.
wählen.
Fitten Sie die untenstehenden Punktreihen nacheinander
(mit der Methode der Fehlergleichungen) nach
1, 2 oder allen 3 der Funktionen
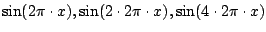
Beachten Sie, dass die bei der kleineren Gruppe
gefundenen Koeffizienten dieselben sind, wie wenn nach einer
größere Anzahl solcher Funktionen gefittet wird.
Dies ist die Eigenschaft der in der Fourier-Zerlegung verwendeten
Funktionen die man Orthogonalität von Funktionen nennt.
-
-
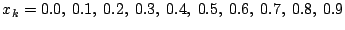
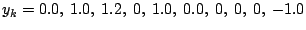




Nächste Seite: Methode der Lagrange-Multiplikatoren
Aufwärts: Übungen zum Kapitel 6
Vorherige Seite: Partielle Ableitungen
Inhalt
Stefan Adam
2006-03-07