



Nächste Seite: Singular Value Decomposition und
Aufwärts: Übungen zum Kapitel 6
Vorherige Seite: Fitprobleme
Inhalt
Unterabschnitte
Stellen Sie die Gleichungen auf, welche das Optimum der Funktion
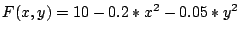 definieren, unter der Bedingung, dass
definieren, unter der Bedingung, dass 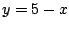 und lösen Sie
das entstehende Gleichungssystem.
und lösen Sie
das entstehende Gleichungssystem.
Suchen Sie das Minimum der Funktion
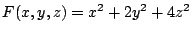
unter der Nebenbedingung
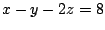
Stellen Sie das nichtlineare Gleichungssystem auf,
welches das Optimum der Funktion
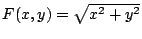 definiert, unter der Bedingung, dass
definiert, unter der Bedingung, dass 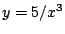 .
.
Die Aufgabe, den höchsten Punkt der Fläche
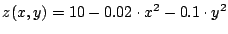 unter der Bedingung
unter der Bedingung 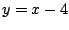 soll mit der Lagrange-Multiplikator-Methode gelöst werden.
soll mit der Lagrange-Multiplikator-Methode gelöst werden.
Dann soll ein Surf- oder Konturplot der Fläche gezeichnet
werden und die 3D-Linie x(t),y(t),z(t), welche auf der Fläche liegt und die
Bedingung erfüllt, soll eingezeichnet werden. Die modifizierte Fläche
mit h=z für y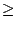 x-4 und 0 für y
x-4 und 0 für y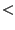 x-4 soll ebenfalls gezeichnet werden.
x-4 soll ebenfalls gezeichnet werden.
Stefan Adam
2006-03-07