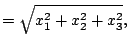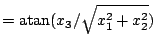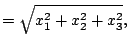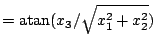Nichtlineare Gleichungssysteme

60-30   Jacobi-Matrix:

 
Bestimmen Sie alle partiellen Ableitungen aller Funktionen 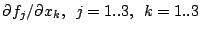$\partial f_j/\partial x_k , ~~j=1 ..3 ,~~ k=1 .. 3$ für die Funktionen:

$$f_1(x_1,x_2,x_3) = \sqrt{x_1^2+x_2^2+x_3^2} ,$$

$$f_2(x_1,x_2,x_3) = \mathrm{atan}(x_2/x_1),$$

$$f_3(x_1,x_2,x_3) = \mathrm{atan}(x_3/\sqrt{x_1^2 +x_2^2})$$

60-31  Nichtlineare Gleichungssysteme

 
Suchen Sie iterativ mit dem zweidimensionalen Newton-Verfahren ab dem Startwert (2,2) eine Lösung des Gleichungssystems

$$(x-4)^2 + y^2 = 10$$

$$x^4 + y^4 = 20$$

60-32   Kugelkoordinaten

 
Die Kugelkoordinaten ergeben ein gutes Beipiel für die Auflösung von nichtlinearen Gleichungssystemen. Bestimmen Sie zu den drei untenstehenden Funktionen von drei Variablen zuerst analytisch die Jacobi-Matrix. Berechnen Sie anschließend 2-3 Verbesserungsschritte, ausgehend vom Schätzwert:

$$x_1 = 4, ~ x_2 = 0.4.~ x_3 = 0.6$$

$$f_1(x_1,x_2,x_3) = x_1 \cdot \cos(x_2) \cdot \cos(x_3) -3$$

$$f_2(x_1,x_2,x_3) = x_1 \cdot \sin(x_2) \cdot \cos(x_3) -1$$

$$f_3(x_1,x_2,x_3) = x_1 \cdot \sin(x_3) -2$$

60-33   Funkfeuerortung

 
Lange vor der Verfügbarkeit des GPS wurden Positionsbestimmungen vorgenommen durch die Auswertung der Zeitdifferenzen zwischen dem Empfang von zeitsynchron ausgestrahlten Signalen mehrerer Funkfeuer, deren Standort man kannte. Dies kann auf die Aufgabe reduziert werden, dass die Differenz d1 der Distanzen zu A(0/0) und B(0/10), sowie d2 zwischen A(0/0) und C(10/0) bekannt ist und daraus die Position (x/y) gesucht wird. Programmieren Sie das Lösungsverfahren nach dem 2D-Newton-Prinzip, um x, y aus d1, d2 zu finden.