



Nächste Seite: Differentialgleichungen höherer Ordnung
Aufwärts: Übungen zum Kapitel 7
Vorherige Seite: Übungen zum Kapitel 7
Inhalt
Unterabschnitte
Eine hervorragende Visualisierung des Lösungsvorgangs bei
Differentialgleichungen ist die Suche des Kurvenverlaufes von
einem Startpunkt aus, in einem Feld von Wegweisern, welche die
lokal gültigen Tangentialrichtungen vorschreiben.
Das Erzeugen eines solchen Wegweiserfeld-Plots ist gleichzeitig eine
einfache Programmierübung. (Empfehlung: Einheiten = cm, Feld 25 cm in x
16 cm in y. Differentialgleichung:
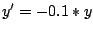 , 2.Fall
, 2.Fall
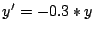 )
)
Lösen Sie die Differentialgleichung
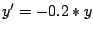 ,
, 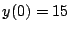 t=0..25
t=0..25
- analytisch
- grafisch, indem Sie in einem Richtungsfeld den Verlauf einzeichnen
- mit MATLAB:
yin = 15;
ysol = ode45('decay02',25, yin);
%und dem function-M-file decay02.m
function deri = decay02(tval,yval);
deri = -0.2* yval;
Programmieren Sie in einem einfachen Skript
die Lösung einer radioaktiven Zerfalls-Gleichung
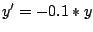 nach
dem Euler-Verfahren
nach
dem Euler-Verfahren
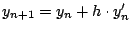 mit konstantem Schritt h.
mit konstantem Schritt h.
Das differentialgleichungssystem 2. Ordnung
eines geladenen Teilchens im konstanten
Magnetfeld
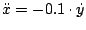 ;
;
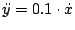 mit
den Anfangsbedingungen
mit
den Anfangsbedingungen 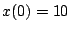 ,
, 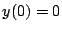 ,
,
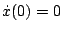 ,
,
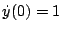 muss zuerst in ein System 1. Ordnung transformiert werden.
Anschließend sollen drei Schritte nach dem Euler-Verfahren
mit Schrittweiten von 0.2 durch Berechnen aller Zwischenresultate
,,von Hand`` berechnet werden.
muss zuerst in ein System 1. Ordnung transformiert werden.
Anschließend sollen drei Schritte nach dem Euler-Verfahren
mit Schrittweiten von 0.2 durch Berechnen aller Zwischenresultate
,,von Hand`` berechnet werden.
Mit Hilfe des Funktions-Aufrufes
fresult = feval('prozedurname',paramater1, parameter2) lässt sich eine
Prozedur zum Lösen eines Differentialgleichungssystems erstellen, welche
dieselbe Signatur aufweist wie die Bibliotheksprozeduren (z.B. ode45()), die
aber nach dem ganz einfache Euler-Verfahren arbeitet. Der Quervergleich
zwischen den
Lösungen mit der selbst erstellten Euler-Lösung und der
Bibliotheksprozedur ode45 zeigt bei Schwingungs-Differentialgleichungen
das interessante Resultat, dass das einfache Verfahren bei genügend
kleiner Schrittweite nur wenig vom professionellen Verfahren abweicht,
und zwar vorwiegend bei der Phasenlage.




Nächste Seite: Differentialgleichungen höherer Ordnung
Aufwärts: Übungen zum Kapitel 7
Vorherige Seite: Übungen zum Kapitel 7
Inhalt
Stefan Adam
2006-03-07