



Nächste Seite: Systeme von Differentialgleichungen
Aufwärts: Übungen zum Kapitel 7
Vorherige Seite: Numerische Lösung von Differentialgleichungen
Inhalt
Unterabschnitte
Die Differentialgleichung des gedämpften, angeregten Oszillators
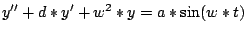 mit z.B. w=2, d= 0.1, a = 0.5
soll zu den Anfangsbedingungen
mit z.B. w=2, d= 0.1, a = 0.5
soll zu den Anfangsbedingungen 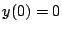 und
und 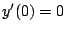 mit MATLAB
gelöst werden. Beachten Sie besonders die Umsetzung in ein System
erster Ordnung durch das Einführen einer neuen Variablen
mit MATLAB
gelöst werden. Beachten Sie besonders die Umsetzung in ein System
erster Ordnung durch das Einführen einer neuen Variablen 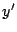 .
Die Regeln für das Erstellen des Funktions-M-Files und der
Aufruf mit vordefinierten Startwerten sind ebenfalls zu beachten!
.
Die Regeln für das Erstellen des Funktions-M-Files und der
Aufruf mit vordefinierten Startwerten sind ebenfalls zu beachten!
yin = [ 0 0 ]' ; [tsol ysol] = ode45('dampedosc',20,yin)
Stellen Sie die Differentialgleichungssysteme auf
für die folgenden Differentialgleichungen höherer Ordnung:
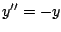
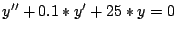
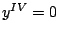
Lösen Sie diese mit MATLAB für die Anfangswerte 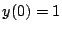 und
und
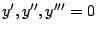 im Bereich
im Bereich 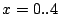
Wenn man der Differentialgleichung für den freien Fall 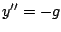 ,
(
,
(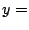 Höhendifferenz zu Startpunkt, immer stärker
negativ werdend, Erdbeschleunigung
Höhendifferenz zu Startpunkt, immer stärker
negativ werdend, Erdbeschleunigung 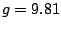 m/s
m/s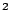 ) einen
Bremsterm proportional zu
) einen
Bremsterm proportional zu
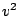 für den
Luftwiderstand beifügt
für den
Luftwiderstand beifügt
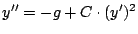 ,
ergibt sich ein Grenzwert für die Fallgeschwindigkeit, der natürlich
stark vom Bremsfaktor abhängt
(Fallschirm, Meteorit, Körperform des Luftakrobaten).
Experimentieren Sie mit dieser Differentialgleichung bei verschiedenen
Bremsfaktoren!
,
ergibt sich ein Grenzwert für die Fallgeschwindigkeit, der natürlich
stark vom Bremsfaktor abhängt
(Fallschirm, Meteorit, Körperform des Luftakrobaten).
Experimentieren Sie mit dieser Differentialgleichung bei verschiedenen
Bremsfaktoren!
Verwenden Sie die Möglichkeit, Variablen die als 'global'
deklariert sind, um die Eigenfrequenz, die
Dämpfung und die Anregungsfrequenz aus dem, den ode-Löser
aufrufenden Skript, in die Ableitungsfunktion hinein zu übermitteln.
Machen Sie damit verschiedene Versuche über die Wirkung der
Dämpfung, und der Differenz zwischen Anregung und Eigenfrequenz.




Nächste Seite: Systeme von Differentialgleichungen
Aufwärts: Übungen zum Kapitel 7
Vorherige Seite: Numerische Lösung von Differentialgleichungen
Inhalt
Stefan Adam
2006-03-07