



Nächste Seite: Spline-Interpolationsfunktionen
Aufwärts: Übungen zum Kapitel 7
Vorherige Seite: Differentialgleichungen höherer Ordnung
Inhalt
Unterabschnitte
Ein einfaches System von 3 Differentialgleichungen je 2. Ordnung
sind die Bewegungen unter alleiniger Wirkung der Schwerkraft:
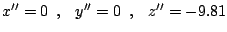 . Die Lösung mit MATLAB ergibt ein
System mit 6 Variablen. Die Anfangsbedingungen können
. Die Lösung mit MATLAB ergibt ein
System mit 6 Variablen. Die Anfangsbedingungen können 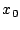 ,
, 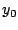 ,
, 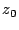 alle Null setzen, die Anfangsgeschwindigkeiten (in m/sec) bestimmen dann
die Flugbahn. (
alle Null setzen, die Anfangsgeschwindigkeiten (in m/sec) bestimmen dann
die Flugbahn. (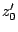 sollte positiv sein und eines der
sollte positiv sein und eines der 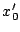 ,
, 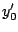 verschieden von 0).
verschieden von 0).
Unter der Annahme, dass beim Start 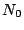 Kerne des Isotopes
Kerne des Isotopes 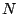 mit der Zerfallskonstanten
mit der Zerfallskonstanten 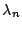 und keine des Tochterkerns M
und keine des Tochterkerns M 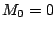 mit
mit 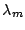 vorhanden sind soll das System von gekoppelten
Differentialgleichungen
vorhanden sind soll das System von gekoppelten
Differentialgleichungen
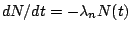 und
und
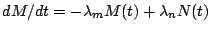 gelöst werden. (Die beim Zerfall des Typs N entstehenden
Tochter-Isotope vom Typ M zerfallen selbst mit der Zeitkonstante
gelöst werden. (Die beim Zerfall des Typs N entstehenden
Tochter-Isotope vom Typ M zerfallen selbst mit der Zeitkonstante 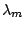 .)
.)
Ein elektrisch geladenes Teilchen im konstanten Magnetfeld
senkrecht zur x-y-Ebene bewegt sich auf einem Kreis.
Demonstrieren Sie diese Tatsache durch Lösen des
Differentialgleichungs-Systems
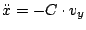 und und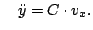 |
|
Berechnen und zeichnen Sie die Bahnen von geladenen Teilchen unter dem Einfluss
eines konstanten Magnetfeldes, das von oben senkrecht in die Tafelebene
zeigt und einem simultanen elektrischen Feld in x-Richtung. Zur
Beschleunigung senkrecht zur momentanen Geschwindigkeit, verursacht durch das
Magnetfeld, wie in der letzten Aufgabe
(
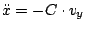 und
und
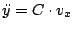 ) kommt eine konstante
Beschleunigung in x-Richtung durch das E-Feld hinzu:
) kommt eine konstante
Beschleunigung in x-Richtung durch das E-Feld hinzu:
Bestimmen Sie aus der allgemeinen Formel für die Lorentz-Kraft
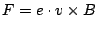 die 3D Bewegung eines geladenen Teilchens
in einem beliebigen konstanten
Magnetfeld (
die 3D Bewegung eines geladenen Teilchens
in einem beliebigen konstanten
Magnetfeld (
![$ [B_x, B_y, B_z]' $](img512.png) ) durch Aufstellen, Transformieren und Lösen der Differentialgleichung.
) durch Aufstellen, Transformieren und Lösen der Differentialgleichung.
Bestimmen Sie die Bahngleichungen einer in einem parabelförmigen Topf
reibungsfrei gleitenden Kugel und integrieren Sie einige Beispielbahnen!




Nächste Seite: Spline-Interpolationsfunktionen
Aufwärts: Übungen zum Kapitel 7
Vorherige Seite: Differentialgleichungen höherer Ordnung
Inhalt
Stefan Adam
2006-03-07