Spline-Interpolationsfunktionen

70-16   Spline-Interpolationsfunktion als Randwertproblem

 
Die Spline-Funktion erfüllt die Differentialgleichung 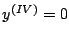$y^{(IV)} = 0$. Suchen Sie die analytische Lösung dieser Differentialgleichung. Diese ergibt ein Polynom 3.Grades, das durch die zwei Stützwerte an den Intervallrändern und die zwei Ableitungen an den Intervallrändern eindeutig bestimmt ist (Randwertproblem).

a)

Stellen Sie die Gleichungen auf für die Bestimmung der Polymomkoeffizienten 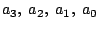$a_3,~a_2,~a_1,~a_0$ (Beispiel-Werte: 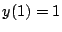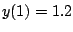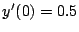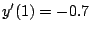$y(1) = 1$, $y(1) = 1.2$, $y'(0) = 0.5$, $y'(1) = -0.7$ ) ausgehend von diesen 4 Werten.

b)

Elementfunktionen: Bestimmen Sie die 4 Elementfunktionen, zur kubischen Spline-Interpolation (jede hat ihre eigenen 4 Koeffizienten), so dass für jede Funktion eine der Bestimmungsgrößen 1 und die andern drei Bestimmungsgrößen = 0 sind.

Die so gefundenen Funktionen sind die Elementfunktionen für eindimensionale finite Elemente.

70-17   Elementarfunktionen der Spline-Interpolation

 
Testen Sie die Symmetrieeigenschaften der elementaren Spline-Funktionen

die Werte entsprechen [y0 y1 y0' y1'].
Formulieren Sie diese Polynome zuerst als Polynome 3. Grades in 't'.
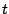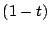Zeigen Sie, dass durch Ersetzen von $t$ durch $(1-t)$ B1 und B2, sowie B3 und B4 ihre Rolle vertauschen.
Faktorisieren Sie diese 4 Polynome und suchen Sie den Zusammenhang zwischen den Faktoren und den Nullstellen mit horizontaler oder schräger Tangente.