Kurven in Parameterdarstellung - mathematische Klassiker

20-14  Verschiedene Zykloiden

 
Erzeugen Sie eine Grafik, in der die normale, gestreckte und die verschlungene Zykloide (Kreis an einer Geraden abrollend, mit verschiedenen Lichtpunktradien) gemeinsam, aber mit verschiedenen Farben dargestellt sind.

20-15   Epizykloide

 
Entwickeln Sie die Formel für die Epizykloide, bei der ein Kreis vom Radius r=1/2*R außen auf einem Kreis vom Radius R abrollt und zeichnen Sie diese Figur anschließend mit MATLAB.

20-16   Hypozykloiden

 
Überlegen Sie sich die Formeln für die 2:1 und 4:1 Hypozykloiden, bei denen ein Kreis vom Radius r=1/2 bzw. r=1/4 im Innern eines Kreises vom Radius 1 abrollt. Zeichnen Sie diese Kurven mit MATLAB.

20-17   Evolvente

 
Entwickeln Sie die Formel für die ,,Faden-Abwickelkurve``. Auf dem Einheitskreis sei ein Faden aufgewickelt. Am Ende des Fadens sei der Schreibstift, so dass er am Anfang im Punkt (1/0) steht. Die Evolvente ergibt sich als Kurvenverlauf des Schreibstiftes, wenn man den Faden beim Abwickeln immer gespannt lässt. (Tangentenabschnittslänge = bisher abgewickelte Bogenlänge.)

20-18   Kepler-Ellipse

 
Zeichnen Sie eine Kepler-Ellipse. (Johannes Kepler, 1571-1630, war der Entdecker der genauen mathematischen Form der Planetenbahnen):
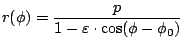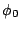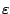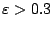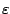$${ r(\phi) = \frac{p}{1-\varepsilon \cdot \cos(\phi-\phi_0)}}$$ . Mit $\phi_0$ bestimmen Sie die Lage der Halbachse, mit $\varepsilon$ die Abweichung von einem Kreis. Empfehlung zum Zeichnen: $\varepsilon > 0.3$. Mit echten Werten von $\varepsilon$ (Erde 0.017, Mars 0.093) sehen Sie keinen Unterschied zu einem Kreis!