Dreidimensionale Kurven in Parameterdarstellung

20-19   Einfache Schraubenlinien

 
Durch den Zusatz eines gleichmäßigen Vorschubes in der z-Richtung entsteht aus einer gleichmäßigen Drehbewegung in der x-y-Ebene (Kreislinie als Lissajous-Figur) eine Schraubenlinie. Erzeugen Sie einen solchen Satz von 3 Vektoren x(w), y(w), z(w) und stellen Sie diese Linie mit plot3(x,y,z) in 3D dar!
Überlegen Sie, wie Sie beeinflussen können, ob die Schraubenlinie linksgängig oder rechtsgängig ist.

20-20   Schraubenlinienpaar bei Parkhausauffahrt

 
Geben Sie ein M-File an, das die beiden Schraubenlinien des linken und rechten Randes der Fahrbahn einer Parkhausauffahrt mit dem Befehl ``plot3(xarray,yarray,zarray)'' grafisch darstellt! Parameter: Durchmesser des inneren Randes = 12 Meter, des äußeren Randes 18 Meter. Einfahrtshöhe = 0 m, Stockwerkabstand = 4 m, 3 Parkebenen plus Parterre.

20-21  Bettfedern

 
Erzeugen Sie für die verschiedenen Varianten von Bettfedern jeweils eine 3D-Parameterdarstellung des räumlichen Verlaufs des zur Feder gebogenen Stahldrahtes. Alle Federn sollen eine Gesamthöhe von 20 cm, einen Maximaldurchmesser von 12 cm und 10 ganze Umgänge aufweisen. Für alle Federn soll der Koordinatenursprung auf der vertikalen Achse bei der Höhe der unteren Begrenzungsebene liegen.
Mark I Zum Anfang kann man eine rein zylindrische Feder, eine sogenannte Wendelfeder annehmen. In diesem einfachen Fall sollten Sie sicherstellen, dass Sie die Links- bzw. Rechtsläufigkeit vorwählen können.
Mark II Der z-Vorschub sollte am Anfang und am Ende deutlich langsamer sein als am Ende. Experimentieren Sie mit verschiedenen Vorschubfunktionen in Abhängigkeit von 't', wie z.B. $z'(t) = Konst.\cdot (1-(t/t_{max})^2 )$,    $z'(t) = Konst.\cdot \sqrt{1-(t/t_{max})^2}$,
$z(t) = Konst.\cdot (1-\cos(2\pi t/t_{max}))$.
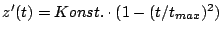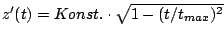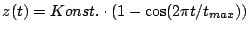Mark III Eine richtige Bettfeder hat in der Mitte einen kleineren Radius als am oberen und unteren Rand. Der Radius kann z.B. mit 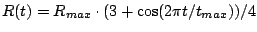$R(t) = R_{max} \cdot (3+\cos(2\pi t/t_{max}))/4$, eventuell kommt auch eine Funktion von z in Frage wie $R(z) = R_{max} \cdot \sqrt{ 0.25 + (0.05\cdot(z-10))^2}$

20-22   Raumkurve einer Wendeltreppe

 
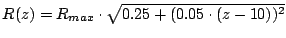
Die Raumkurve einer Wendeltreppe mit Innenradius 20 cm und Außenradius 180 cm lässt sich von der Schraubenlinie ableiten. Die Stufenhöhe soll gleichmäßig 24 cm betragen und die Treppe in einem Umgang 288 cm Höhe überwinden. Beachten Sie dass für das Erzeugen des Treppeneffektes immer zweimal dieselben x-y Positionen bei steigendem z-Wert und dann derselbe z-Wert bei verschiedenen Winkeln vorkommen.