Lineare Abhängigkeit

30-1   Paarweise lineare Unabhängigkeit

 

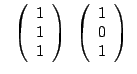
Konstruieren Sie zu der nebenstehenden Zweiergruppe von Vektoren einen dritten, so dass je zwei der Vektoren linear unabhängig sind, aber alle drei linear abhängig.
Hinweis: Streben Sie an, durch Linearkombinationen mit Probieren den Nullvektor zu erzeugen. Gelingt dies, so sind die Vektoren linear abhängig, ist dies unmöglich, so sind die Vektoren linear unabhängig.

 

$~~~\left(\begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right) ~~ \left(\begin{array}{c} 1 \\ 0 \\ 1 \end{array} \right) ~~$

30-2   Linear unabhängige Dreiergruppen

 

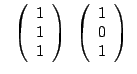
Die nebenstehende Gruppe von drei Vektoren ist linear unabhängig. Durch einen speziell gewählten vierten Vektor soll die Vierergruppe linear abhängig sein.
Anders zusammenstellbare Dreiergruppen sollen dagegen unabhängig sein.

 

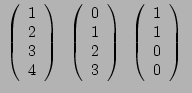
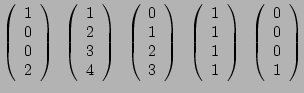$~ \left(\begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \end{array} \right) ~~ \left(\be... ... \right) ~~ \left(\begin{array}{c} 1 \\ 1 \\ 0 \\ 0 \end{array} \right) ~~$

30-3   Lineare Abhängigkeiten bei einer Gruppe von Spaltenvektoren

 
Suchen Sie unter den untenstehenden Vektoren möglichst große Gruppen, die voneinander linear unabhängig sind! Hinweis: durch Aneinanderfügen von Vektoren können Sie in MATLAB Matrizen erzeugen, deren Rang Sie mit der Funktion rank() bestimmen können.

$$\left(\begin{array}{c} 1 \\ 0 \\ 0 \\ 2 \end{array} \right) ~~ \l... ...d{array} \right) ~~ \left(\begin{array}{c} 0 \\ 0 \\ 0 \\ 1 \end{array} \right)$$