



Nächste Seite: Lösung von angewandten Textaufgaben
Aufwärts: Übungen zum Kapitel 3
Vorherige Seite: Lineare Abhängigkeit
Inhalt
Unterabschnitte
Bestimmen Sie jeweils den Rang aller möglichen
Sets von 4 aus den
gegebenen Vektoren ausgewählten Vektoren.
Die Reihenfolge der Anordnung ist für den Rang unwichtig;
kontrollieren Sie diese Aussage an zwei bis drei Beispielen.
Suchen Sie Werte für 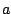 und
und 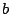 , so dass der Rang der untenstehenden
Matrix möglichst groß, bzw. möglichst klein wird.
, so dass der Rang der untenstehenden
Matrix möglichst groß, bzw. möglichst klein wird.
Bestimmen Sie für die untenstehenden Vektorgruppen jeweils Wertebereiche
für die Parameter 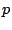 und
und 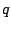 , so dass eine Gruppe linear unabhängig,
bzw. dass sie möglichst stark linear abhängig ist (Maximalrang=Vollrang,
bzw. Minimalrang).
, so dass eine Gruppe linear unabhängig,
bzw. dass sie möglichst stark linear abhängig ist (Maximalrang=Vollrang,
bzw. Minimalrang).
a)
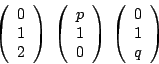 b)
b)

Stefan Adam
2006-03-07
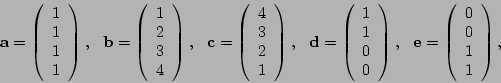
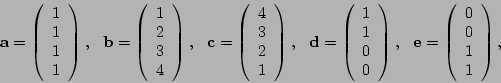

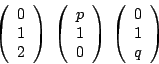 b)
b)
