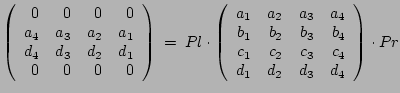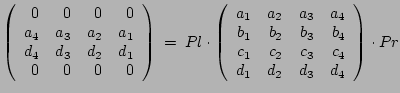Nächste Seite: Orthogonale Matrizen
Aufwärts: Übungen zum Kapitel 3
Vorherige Seite: Funktions-M-Files
Inhalt
Unterabschnitte
Füllen Sie eine 4x4 Matrix M der Reihe nach mit den Zahlen 1 .. 16.
Erzeugen Sie eine andere 4x4 Matrix S mit lauter Nullen, außer einer einzigen
Eins. Beobachten Sie den Effekt, den die Multiplikationen
S*M und M*S produzieren für verschieden gewählte
Positionen der Eins innerhalb von S!
Erstellen Sie als Testobjekt T eine 5x5 Index-Anzeige-Matrix
(mit zweistelligen
Zahlen die den Indizes entsprechen, z.B. 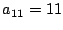 ,
,
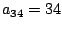 )
)
Multiplizieren Sie diese mit der geeigneten Spechtmatrix von links her,
mit dem Ziel, die erste Zeile von T in die 1., 2., 4. und 5. Zeile
zu platzieren.
Bestimmen und testen Sie ebenso die notwendigen Spechtmatrizen
für eine analoge Platzierung der 4. und der 5. Zeile von T.
Verwenden Sie wieder als Testobjekt T eine 5x5 Index-Anzeige-Matrix.
Multiplizieren Sie diese Matrix mit der geeigneten Spechtmatrix
von rechts her,
mit dem Ziel, die erste Spalte von T in die 1., 2., 4. und 5. Spalte
der Resultatmatrix
zu platzieren.
Bestimmen und testen Sie ebenso die notwendigen Spechtmatrizen
für eine analoge Platzierung der 4. und der 5. Spalte von T.
Quadratische (nxn), sogenannte ,,Turmmatrizen`` haben in jeder
Zeile und in jeder Kolonne
genau eine Eins und sonst lauter Nullen.
(So könnte man Türme auf ein Schachbrett stellen,
die sich gegenseitig nicht bedrohen.)
Diese Matrizen vertauschen die Reihenfolge der Zeilen von Matrizen die
damit multipliziert werden.
Erzeugen Sie einige Beispiele von solchen Matrizen und überzeugen Sie sich
davon, dass: - 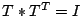 ist; - alle T orthogonal sind. Das Produkt
einer orthogonalen Matrix mit Ihrer Transponierten ergibt die Einheitsmatrix.
ist; - alle T orthogonal sind. Das Produkt
einer orthogonalen Matrix mit Ihrer Transponierten ergibt die Einheitsmatrix.
Potenzieren Sie die in der vorherigen Übung erstellten Turmmatrizen
mit ganzzahligen Exponenten. Welches ist der kleinste
Exponent, bei welchem 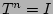 wird?
wird?
Dieser kleinste Exponent kann nie größer als die Dimension sein!
Da die Anzahl möglicher Permutationen bei größerem 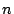 rasant ansteigt
rasant ansteigt
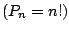 , ergäbe es eine Riesenarbeit, alle möglichen
Permutationsmatrizen aufzuschreiben.
Versuchen Sie ein MATLAB-Programm zu schreiben, das mit Hilfe der
Zufallsfunktion eine Turmmatrix erzeugt, d.h., das die Zufallsfunktion
rand(1) benutzt, um eine Turmmatrix zu vorgegebener Dimension
, ergäbe es eine Riesenarbeit, alle möglichen
Permutationsmatrizen aufzuschreiben.
Versuchen Sie ein MATLAB-Programm zu schreiben, das mit Hilfe der
Zufallsfunktion eine Turmmatrix erzeugt, d.h., das die Zufallsfunktion
rand(1) benutzt, um eine Turmmatrix zu vorgegebener Dimension 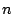 festzulegen.
festzulegen.
Erstellen Sie ein MATLAB-Programm (als Funktions-M-File), das einen
Spaltenvektor mit den Zahlen von 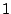 bis
bis 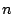 in beliebiger Reihenfolge als
Eingabe benötigt, und daraus diejenige Turmmatrix produziert, welche die im
Eingabevektor enthaltene Permutation erzeugt. Als Test kann die
Multiplikation der Turmmatrix von links an einen Vektor mit der
natürlichen Abfolge der Zahlen
in beliebiger Reihenfolge als
Eingabe benötigt, und daraus diejenige Turmmatrix produziert, welche die im
Eingabevektor enthaltene Permutation erzeugt. Als Test kann die
Multiplikation der Turmmatrix von links an einen Vektor mit der
natürlichen Abfolge der Zahlen
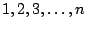 dienen. Durch diese
Multiplikation soll der vorgegebene Vektor erzeugt werden.
dienen. Durch diese
Multiplikation soll der vorgegebene Vektor erzeugt werden.
Spezielle Turmmatrizen sind die Scroll-up-
(bzw. Scroll-down)-Matrizen (fast alle Einsen direkt oberhalb/ unterhalb
der Diagonalen). Bei der Multiplikation von links schieben Sie alle Zeilen
der rechts stehenden Matrix (alle Werte eines rechts stehenden Vektors)
um einen Platz nach oben (bzw. unten). Wird das am Rand herausfallende
Element am anderen Rand eingefüllt, so nennt man die Scroll-up/down-Abbildung zyklisch. Fällt das Element am Rand weg, so sind die Matrizen
keine eigentlichen Turmmatrizen mehr.
Erstellen Sie für die Dimension 5 alle 4 Typen: zyklische und nicht
zyklische Scroll-up- und Scroll-down-Matrizen und testen Sie
deren Wirkung an einem Spaltenvektor mit den Zahlen 1:5.
Überlegen Sie sich, welchen Rang diese 4 Matrizen haben
und kontrollieren Sie
Ihr Resultat mit MATLAB.
Testen Sie die Wirkung einiger Turmmatrizen (insbesondere der Sroll up/down
Matrizen) beim Multiplizieren der Index-Anzeige-Matrix von links her und
von rechts her.
Bestimmen Sie die Matrizen 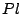 und
und 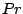 so, dass
für beliebige
so, dass
für beliebige
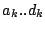 gilt:
gilt:
Turmmatrizen, welche sich nur an zwei Stellen von einer
Einheitsmatrix unterscheiden: Beinahe-Einheitsmatrizen
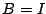 , außer
, außer
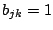 ,
,
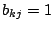 und
und
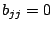 ,
,
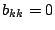 bewirken nur eine einzige Permutation
zwischen j und k. Aus Produkten von solchen Elementarpermutationen
kann man jede Turmmatrix herstellen. Für jede B-Matrix gilt
bewirken nur eine einzige Permutation
zwischen j und k. Aus Produkten von solchen Elementarpermutationen
kann man jede Turmmatrix herstellen. Für jede B-Matrix gilt
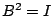 . Testen Sie diese beiden Eigenschaften an einfachen Beispielen, z.B.
an der Permutation [4 3 2 1] aus [1 2 3 4], bzw. an den Paaren
j,k = 1,2, oder 1,4, oder 2,4.
. Testen Sie diese beiden Eigenschaften an einfachen Beispielen, z.B.
an der Permutation [4 3 2 1] aus [1 2 3 4], bzw. an den Paaren
j,k = 1,2, oder 1,4, oder 2,4.
Bestimmen Sie zwei 4x4 Turmmatrizen Tl und Tr, (eine von
links und eine von rechts zu
multiplizierende) so, dass dadurch ( mit Tl*A*Tr)
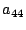 an die linke obere Ecke
und
an die linke obere Ecke
und 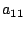 an die rechte untere Ecke verschoben werden!
an die rechte untere Ecke verschoben werden!




Nächste Seite: Orthogonale Matrizen
Aufwärts: Übungen zum Kapitel 3
Vorherige Seite: Funktions-M-Files
Inhalt
Stefan Adam
2006-03-07