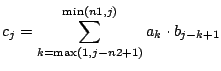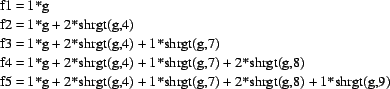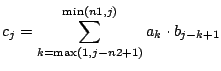Nächste Seite: Zirkuläre Faltungen
Aufwärts: Übungen zum Kapitel 5
Vorherige Seite: Übungen zum Kapitel 5
Inhalt
Unterabschnitte
Berechnen Sie die Faltungen conv(a,b), conv(b,a), conv(a,a) und
conv(b,b) von Hand und mit MATLAB:
-
- a = [ 1 2 1 2 1] , b = [0 0 1 3 1 0 0]
Falten Sie die Rechtecksfunktion a = [ 0 0 0 1 1 1 1 0 0 0]
ein- bis mehrmals mit sich selbst und vergleichen Sie die grafischen
Darstellungen der Folgen.
Gegeben sind die zwei Zahlenfolgen (der Länge 14) g und w durch
-
- g = [ 1 2 3 2 1 zeros(1,9) ]
w = [ 0 0 1 0 0 0 2 0 0 1 2 1 0 0 ]
Erzeugen Sie eine Shift-Funktion,
mit der Sie den von Null verschiedenen Teil
von g nach rechts
verschieben können ohne die Länge zu ändern, z.B. wird:
-
- shrgt(g,4) = [ 0 0 0 0 1 2 3 2 1 0 0 0 0 0]
Mit dieser Shift-Funktion kann die Faltung als schrittweise
Addition von zueinander verschobenen Folgen g, je mit entsprechenden
Gewichten w(k) nachvollzogen werden.
Die Zahlenfolgen f1 bis f4 bilden dann die Teilresultate und f5 das
Schlussresultat
der Faltung von g und w. Diese sollen übereinander geplottet werden:
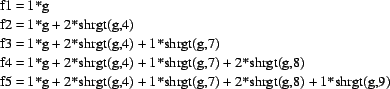
f5 kann anschließend mit der MATLAB-Funktion für die Faltung
verglichen werden: conv(g,w)
Falten Sie die vier Standardfunktionen: Rechtecks-, (Dreiecks=)
Hutfunktion, Parabelbogen (
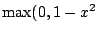 ) und Glockenfunktion
(
) und Glockenfunktion
(
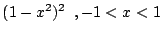 ) je mit sich selbst, sowie
mit der Rechtecks und der Hutfunktion und stellen Sie die
Original- und Resultatfunktionen grafisch dar.
) je mit sich selbst, sowie
mit der Rechtecks und der Hutfunktion und stellen Sie die
Original- und Resultatfunktionen grafisch dar.
Berechnen und zeichnen Sie die zirkuläre
Faltung einer Sinusfunktion mit sich selbst.
Erzeugen Sie ein Funktions-M-File, das eine Faltung
von 2 Folgen berechnet, indem die verschobenen und mit dem Gewicht
multiplizierten Vektoren sukzessive addiert werden.
Erzeugen Sie dazu eine intern zu verwendende Hilfsfunktion, welche
einen Vektor an einem vorwählbaren Platz in einen längeren
Nullvektor einsetzt, wie z.B.
-
- bigvec = vecinsert(smallvec,lpos,biglength)
Schreiben Sie ein MATLAB-Skript, welches eine gewöhnliche Faltung
programmiert. Diese ist durch die untenstehende Formel gegeben.
Vergleichen Sie die Resultate Ihres Skripts mit der Bibliotheksprozedur
C=conv(A,B)! Testen Sie auch die Symmetrieeigenschaft
der Faltung und die Länge der Resultatfolge an einigen Beispielen!
Beachten Sie, dass die sprachliche Formulierung ,,j-n2+1,
aber mindestens 1``
mit der Funktion max(1,j-k+1) realisiert
wird (nicht mit ,,min``
was die sprachliche Form suggeriert)!




Nächste Seite: Zirkuläre Faltungen
Aufwärts: Übungen zum Kapitel 5
Vorherige Seite: Übungen zum Kapitel 5
Inhalt
Stefan Adam
2006-03-07