Zirkuläre Faltungen

50-8   Zirkuläre Faltung mit einfacher Schleife

 
Unter Verwendung des untenstehenden Funktions-M-Files shrgt.m :
function vecret = shrgt(vecin, nshift)
ntot = length(vecin); nlast = ntot - nshift ;
vecret = [ vecin(nlast+1:ntot) , vecin(1:nlast)]; 
soll eine zirkuläre Faltung allgemein für die zwei gleich langen Folgen a und b durch eine einzelne Schleife programmiert werden.

Ausblick: Versuchen Sie shrgt.m so umzuprogrammieren, dass die Funktion robuster wird, d.h. dass negative Werte, Null oder zu große Werte von nshift erlaubt sind und sinnvoll umgesetzt werden!

50-9   Zirkuläre Faltung mit doppelter Schleife

 
Programmieren Sie eine Doppelschleife mit Bedingungen, so dass eine allgemeine zirkuläre Faltung entsprechend der Summenformel im Theorieteil berechnet wird (Ausprogrammieren einer Formel).

50-10   Faltung einer Sinus-Funktion mit sich selbst:

 
Berechnen und Zeichnen Sie die Zirkuläre Faltung einer Sinus-Funktion mit sich selbst.

50-11   Zirkuläre Faltung mit Faltungssatz

 
Testen Sie den Faltungssatz am Beispiel der zirkulären Faltung der beiden Folgen a = [ 1 2 3 4 5 6] und b = [1 0 0 1 0 0] und berechnen Sie die zirkuläre Faltung zur Kontrolle von Hand.

Der Faltungssatz sagt aus, dass eine zirkuläre Faltung durch je eine Fourier-Transformation der Ausgangsfolgen, eine elementweise Multiplikation (genannt Hadamard-Produkt) der beiden Fourier-Transformierten und eine anschließende Rücktransformation ersetzt werden kann:

50-12   Funktions-M-File für zirkuläre Faltung mit FFT

 
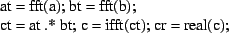
Ergänzen Sie die untenstehende Berechnungsvorschrift zu einem lauffähigen Funktions-M-File in MATLAB und berechnen Sie damit die zirkuläre Faltung für einige Beispiele. Testen Sie, wieviele Nullen Sie an jede der Eingangsfolgen anhängen müssen, damit Sie die normale Faltung bekommen. Weisen Sie auch nach, dass die Nullen am Anfang oder Ende angehängt werden können!

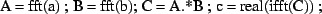
Erhöhen Sie die Robustheit Ihrer Funktion durch Angleichen der Länge bei Eingabefolgen verschiedener Länge.

50-13   Normale Faltung auf zirkuläre Faltung zurückführen

 
Führen Sie die normale Faltung der Folgen a = [ 1 2 3 2 1] und b = [1 2 1 1 1 2 1] aus. Finden Sie heraus, wieviele Nullen (zero padding) Sie an jede der Folgen mindestens anhängen müssen, dass die zirkuläre Faltung der verlängerten ap und bp via Schnelle Fourier-Transformation dasselbe ergibt.

cr = real( ifft(fft(ap).*fft(bp)) ) ;

50-14   Vergleich von zirkulärer und gewöhnlicher Faltung

 
Zeichnen Sie die beiden Resultate der zirkulären und der gewöhnlichen Faltung der beiden Folgen a=[1 2 3 4 5 4 3 2 1] und b = [0 1 1 1 1 1 1 1 0]. Beachten Sie, dass bei der zirkulären Faltung kein auslaufender Rand entsteht.