



Nächste Seite: Das Prinzip des FFT-Algorithmus
Aufwärts: Übungen zum Kapitel 5
Vorherige Seite: Zirkuläre Faltungen
Inhalt
Unterabschnitte
Erstellen Sie ein Funktions-M-File mit den Eingabeparametern
n, A, B und k, das eine Zahlenfolge der Länge n erzeugt, welche
der Funktion
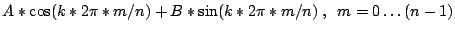 entspricht.
entspricht.
Testen Sie an einigen Beispielen (nach Vorwahl von 'n') die Werte
für sum(sico(n,1,0,ka).*sico(n,1,0,kb)) für gleiche
und für verschiedene 'ka', 'kb'. (= Skalarprodukt von Funktionen).
Ebenso sollten sum(sico(n,1,0,ka).*sico(n,0,1,kb)) für
beliebige 'ka', 'kb' immer Null geben.
Was bedeutet der Zahlenwert, den Sie beim Skalarprodukt von zwei
identischen Folgen erhalten?
Sehen Sie sich die Resultatgrafiken des MATLAB-Skripts
foudem.m
für verschiedene Eingangsfunktionen an (fdefXXX.m können
verschiedene Zeitfunktionen, alle mit dem Namen 'f' definiert werden).
Beachten Sie besonders, dass:
- -
- gerade Funktionen nur cos-Koeffizienten und
- -
- ungerade nur sin-Koeffizienten aufweisen,
- -
- Phasenverschiebungen die Gesamtamplitude konstant halten, aber
die Anteile von sin und cos verändern, und dass
- -
- bei steileren Flanken der Zeitfunktion
die Amplituden der höheren Harmonischen zunehmen.
Betrachten Sie im Demo-Skript
foushow.m
die verschiedenen
Darstellungsarten von Fourier-Transformierten!
(benötigt rearrg.m)
Die meisten der dazugehörenden
Funktionen sind selbsterklärend.
-
- fdefnarrpeak.m ,
fdefmedpeak.m ,
fdefwidpeak.m ,
fdefsquare.m
ergeben verschieden breite Rechteckpeaks,
-
- fdefsin.m ,
fdefcos.m
,
ergeben die Elementarfunktionen und
-
- fdeftriang.m ,
fdefsaegz.m
,
sowie
fdefhat.m
ergeben verschiedene Arten von Dreiecksfunktionen.
Erzeugen Sie eine Funktion zum Herstellen von Zahlenreihen, welche
Rechteckpulse darstellen. Als Eingabeparameter benötigen Sie
die Anzahl Punkte, die linke Flanke und die rechte Flanke.
Betrachten Sie jeweils mit foushow.m die Effekte einer
Breitenänderung und einer Positionsänderung des Rechteckpeaks.
Überlegen Sie sich in jedem Fall vorher, was Sie als Resultat erwarten,
und versuchen Sie die Fälle zu verstehen, in denen Ihre Prognose
falsch war.
Das Skript
foushow.m
(benötigt
rearrg.m
)
zeigt alle Darstellungen nacheinander: die Fourier-Koeffizienten
für cos und sin, dann die direkten Resultate der fft (fast fourier
transform, ohne Normierung) und dann die Darstellung mit negativen und
positiven Frequenzen.
In der Darstellung mit negativen und positiven Frequenzen
müssen die Realteile der Koeffizienten symmetrisch zur y-Achse
sein (gerade Funktion) und die Imaginärteile punktsymmetrisch zum
Ursprung, damit eine reelle Zeitfunktion dargestellt wird.
Dann stimmen nämlich die Euler'sche Relation
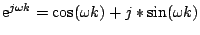 und die daraus abgeleiteten
Formeln
und die daraus abgeleiteten
Formeln
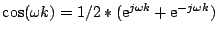 und
und
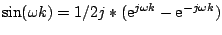 .
.
Mit
foushowexp.m
(benötigt ebenfalls
rearrg.m
) erhalten Sie direkt diese Darstellung.
Wenn zu einer Funktion die Fourier-Koeffizienten bestimmt werden, und
diese vor der Synthese ab einer bestimmten Frequenz abrupt Null gesetzt
werden, so entsteht das Gibbs'sche Phänomen, ein Überschwingen der
rekonstruierten Funktion bei den steilen Flanken der Originalfunktion.
Dies kann mit dem M-File
fclipm.m
demonstriert werden.
Wie dieser Effekt durch ein sanftes Auslaufen der
Fourier-Koeffizienten (mit Hilfe der Lanczos-Faktoren)
vermieden werden kann, zeigt das Skript
fclipla.m
.




Nächste Seite: Das Prinzip des FFT-Algorithmus
Aufwärts: Übungen zum Kapitel 5
Vorherige Seite: Zirkuläre Faltungen
Inhalt
Stefan Adam
2006-03-07