



Nächste Seite: Matrixdefinition
Aufwärts: Übungen zum Kapitel 1
Vorherige Seite: Produktschreibweise mit '*'
Inhalt
Unterabschnitte
Der Mathematiker Karl Friedrich Gauß sollte als Primarschüler mit der Aufgabe
beschäftigt werden, alle Zahlen von 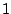 bis und mit
bis und mit 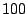 zusammenzuzählen. Da
er sofort das Prinzip herausfand, dass jede Zusammenfassung einer Zahl aus der
unteren Hälfte mit einer passenden aus der oberen Hälfte den Wert
zusammenzuzählen. Da
er sofort das Prinzip herausfand, dass jede Zusammenfassung einer Zahl aus der
unteren Hälfte mit einer passenden aus der oberen Hälfte den Wert 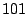 ergab,
und dass es
ergab,
und dass es 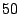 solche Paare gab, fand er sehr schnell
das Resultat
solche Paare gab, fand er sehr schnell
das Resultat
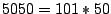 .
.
Die allgemeine Formel für die Summe einer Reihe natürlicher Zahlen von 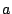 bis
bis
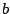 lautet
lautet
Testen Sie diese Formel, indem Sie verschiedene Reihen mit dem Befehl
r = a:b erzeugen und deren Summe mit sum(r), sowie mit der
obigen Formel berechnen.
Eine allgemeine arithmetische Reihe ist definiert durch
die Formel für das allgemeine Element:
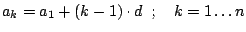 .
.
Die zugehörige
Summenformel lautet:
Verwenden Sie wiederum den impliziten Schleifenoperator : (diesmal
in der Form a:d:b), um
verschiedene arithmetische Reihen zu erzeugen und anschließend
deren Summe mit sum(r) zu berechnen. Vergleichen Sie jeweils den
so bestimmten Summenwert mit dem Resultat der Formelauswertung!
(Mögliche Beispielwerte sind
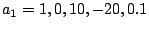 ,
,
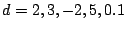 und
und
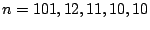 .)
.)
Trotz des Vorfaktors 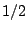 wird das Resultat für ganzzahlige
wird das Resultat für ganzzahlige 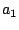 und
und
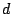 immer ganzzahlig; ein ganz kleines mathematisches Wunder!
immer ganzzahlig; ein ganz kleines mathematisches Wunder!
Ein magisches Quadrat der Dimension nxn enthält alle natürlichen
Zahlen zwischen 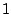 und
und 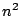 . Der Wert der überall gleichen Zeilen-
und Spaltensummen lässt sich aus folgender Überlegung bestimmen:
er muss
. Der Wert der überall gleichen Zeilen-
und Spaltensummen lässt sich aus folgender Überlegung bestimmen:
er muss 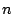 mal dem Durchschnittswert aller Elemente entsprechen.
Berechnen Sie diesen Summenwert für
mal dem Durchschnittswert aller Elemente entsprechen.
Berechnen Sie diesen Summenwert für
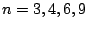 !
!




Nächste Seite: Matrixdefinition
Aufwärts: Übungen zum Kapitel 1
Vorherige Seite: Produktschreibweise mit '*'
Inhalt
Stefan Adam
2006-03-07
![]() bis
bis
![]() lautet
lautet