



Nächste Seite: Kirchhoff'sche Netze mit stationären
Aufwärts: Übungen zum Kapitel 3
Vorherige Seite: Lösung von angewandten Textaufgaben
Inhalt
Unterabschnitte
Berechnen Sie die Ströme im untenstehenden Netzwerk (alle R in Ohm):
*---------------*----100----*----250----*
| | | |
| 200 100 100
| | | |
= 10 V *----200----*---100-----*
| | |
| 100 50
| | |
*---------------*----250----*
Ein elektrisches Netzwerk hat 6 Knoten. Die Einspeisung erfolgt
zwischen Knoten 1 (+10 V) und Knoten 6 (0 V).
Die Verbindung und ihre Widerstände sind: 1-2, 2-3 100 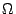 ;
1-4 200
;
1-4 200 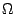 ; 2-5 400
; 2-5 400 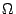 ; 3-6 1 k
; 3-6 1 k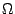 ;
4-5 100
;
4-5 100 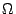 ; 5-6 500
; 5-6 500 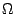 .
Berechnen Sie den Ersatzwiderstand und die einzelnen Ströme!
.
Berechnen Sie den Ersatzwiderstand und die einzelnen Ströme!
Berechnen Sie mit den Kirchhoff'schen Regeln und der Hilfe von MATLAB
die Ersatzwiderstände der Dreieckstrukturen
mit je 100 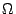 in den einzelnen Zweigen:
in den einzelnen Zweigen:
Erstellen Sie ein M-File für die Berechnung des Stromes im
Messzweig
einer Wheatstone'schen Brücke mit 0.01 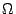 im Galvanometerzweig
(= Messzweig)
und den allgemein vor der Abarbeitung des M-Files definierten
Widerständen R1, R2 (oberer Zweig) und R3, R4 (unterer Zweig).
Experimentieren Sie mit verschiedenen Werten von R1 bis
R4, um sich von der Abgleicheigenschaft zu überzeugen:
I5=0, falls R1:R2 = R3:R4.
im Galvanometerzweig
(= Messzweig)
und den allgemein vor der Abarbeitung des M-Files definierten
Widerständen R1, R2 (oberer Zweig) und R3, R4 (unterer Zweig).
Experimentieren Sie mit verschiedenen Werten von R1 bis
R4, um sich von der Abgleicheigenschaft zu überzeugen:
I5=0, falls R1:R2 = R3:R4.
Berechnen Sie den Ersatzwiderstand entlang der Diagonalen
für ein Widerstandsnetz,
das an allen Kanten und Unterteilungslinien eines in 4 (bzw. 9 , 16)
Teilquadrate unterteilten Quadrates je einen Widerstand von 1 k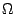 aufweist.
aufweist.




Nächste Seite: Kirchhoff'sche Netze mit stationären
Aufwärts: Übungen zum Kapitel 3
Vorherige Seite: Lösung von angewandten Textaufgaben
Inhalt
Stefan Adam
2006-03-07
![\includegraphics[width=7.5cm, clip]{img/kirchtriang}](img180.png)
![\includegraphics[width=7.5cm, clip]{img/kirchtriang}](img180.png)