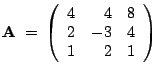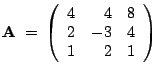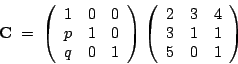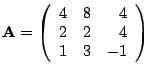Nächste Seite: Miniprojekte zur linearen Algebra
Aufwärts: Übungen zum Kapitel 3
Vorherige Seite: Orthogonale Matrizen
Inhalt
Unterabschnitte
Sehen Sie sich die Demo-Programme showgauss.m und showlr.m für verschiedene
Matrizen und rechte Seiten an, und zwar immer für eine
Matrix M und einen Vektor b
zuerst showgauss(M,b) und anschließend
showlr(M).
Die beiden Files sind im Anhang ,,B.3 M-Files zur
Linearen Algebra`` und auf der
Begleit-CD zu finden.
Erstellen Sie ein MATLAB-Script, welches für eine bereits teilweise
in R-Form überführte Matrix in der Spalte k die möglichen
Pivot-Elemente vergleicht, das betragsmäßig Größte sucht und die
entsprechenden Teilzeilen miteinander vertauscht (=Zwischenschritt
am Anfang jeder Spaltenverarbeitung).
Programmieren Sie die Lösung durch Rückwärtseinsetzen für ein Gleichungssystem
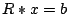 . Vom Gleichungssystem wird die spezielle Eigenschaft vorausgesetzt,
dass die Rechts-Dreiecksmatrix
. Vom Gleichungssystem wird die spezielle Eigenschaft vorausgesetzt,
dass die Rechts-Dreiecksmatrix 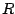 nur in der Diagonalen und in der direkt zur
Diagonalen benachbarten Linie (d.h. der oberen Nebendiagonalen) Elemente mit
Werten verschieden von Null aufweist.
nur in der Diagonalen und in der direkt zur
Diagonalen benachbarten Linie (d.h. der oberen Nebendiagonalen) Elemente mit
Werten verschieden von Null aufweist.
Führen Sie die einzelnen Schritte der Gauß-Elimination
für die untenstehende Matrix mit Bleistift und Papier aus.
Erzeugen Sie aus den Kombinationskoeffizienten die Teilmatrizen L1 und L2,
so dass gilt:
1. Schritt:
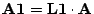 ,
2. Schritt:
,
2. Schritt:
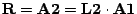
insgesamt:
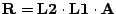
Bilden Sie anschließend mit MATLAB die Matrizen 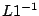 und
und 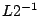 und zeigen Sie, dass die von der Bibliotheksprozedur
[L,R,P] = lu(A)
gelieferte Matrix L dem Produkt
und zeigen Sie, dass die von der Bibliotheksprozedur
[L,R,P] = lu(A)
gelieferte Matrix L dem Produkt
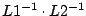 entspricht!
entspricht!
Bestimmen Sie in der untenstehenden Matrizengleichung die Parameter
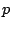 und
und 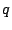 so, dass die Elemente
so, dass die Elemente 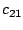 und
und 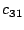 der Resultatmatrix
der Resultatmatrix
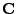 Null werden!
Null werden!
Eine 3x3 R-Matrix hat die Werte [ 1 2 3 ; 0 4 5 ; 0 0 6 ].
Die Multiplikationsfaktoren in der Gauß-Elimination waren von oben
nach unten in der ersten Spalte 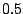 und
und 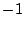 , in der zweiten Spalte
, in der zweiten Spalte 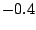 .
Wie lautete die Originalmatrix
.
Wie lautete die Originalmatrix 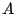 ?
?
Bestimmen Sie die zwei Zerlegungsmatrizen L und R
zur untenstehenden Matrix A mit der Bibliotheksfunktion
[L,R,P] = lu(A). Bestimmen Sie anschließend die drei
Lösungsvektoren zu den rechten Seiten [1 0 0]', [0 1 0]',
[0 0 1]' durch Vorwärts-/Rückwärtseinsetzen in L und R von Hand.
Damit haben Sie die Spaltenvektoren von 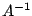 berechnet.
Testen Sie dies durch die Multiplikation
berechnet.
Testen Sie dies durch die Multiplikation
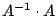




Nächste Seite: Miniprojekte zur linearen Algebra
Aufwärts: Übungen zum Kapitel 3
Vorherige Seite: Orthogonale Matrizen
Inhalt
Stefan Adam
2006-03-07